题目内容
14.(x2+mx+8)(x2-3x+n)展开后不含x2和x3的项,则m、n的值为( )| A. | m=3,n=1 | B. | m=0,n=0 | C. | m=-3,n=-9 | D. | m=-3,n=8 |
分析 根据多项式乘以多项式的法则先把要求的式子进行整理,再根据多项式展开后不含x2和x3的项,得出-3+m=0,n-3m+8=0,求出m,n的值即可.
解答 解:∵(x2+mx+8)(x2-3x+n)=x4-3x3+x2n+x3m-3mx2+mnx+8x2-24x+8n=x4+(-3+m)x3+(n-3m+8)x2+mnx-24x+8n,
又∵(x2+mx+8)(x2-3x+n)展开后不含x2和x3的项,
∴-3+m=0,n-3m+8=0,
∴m=3,n=1;
故选A.
点评 本题考查了多项式乘多项式,理解不含x2和x3的项,即二次项次数与三次项系数都是0是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.生物学家发现一种病毒的长度约为0.00004mm,用科学记数法表示是( )
| A. | 0.4×10-4 | B. | 4×10-5 | C. | 40×10-5 | D. | 4×105 |
2.已知(x-3)2+|y-4|=0,则$\frac{x}{y}$的算术平方根是( )
| A. | $±\frac{{\sqrt{3}}}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{\sqrt{3}}}{4}$ | D. | $±\frac{{\sqrt{3}}}{4}$ |
19.下列运算正确的是( )
| A. | $\sqrt{18}÷\sqrt{2}=9$ | B. | ${(\frac{1}{3})}^{-2}=\frac{1}{9}$ | C. | (-a2)3=a6 | D. | a6÷($\frac{1}{2}$a2)=2a4 |
4.下列各数没有平方根的是( )
| A. | 0 | B. | |-2| | C. | -4 | D. | -(-5) |
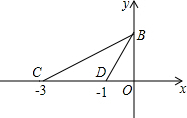 如图,在平面直角坐标系中,C(-3,0),D(-1,0),点B在y轴正半轴上,且tan∠BCO=$\frac{\sqrt{3}}{3}$
如图,在平面直角坐标系中,C(-3,0),D(-1,0),点B在y轴正半轴上,且tan∠BCO=$\frac{\sqrt{3}}{3}$ 如图是一个长方形纸条折成的图形,已知图中∠2=122°,则∠1=116°.
如图是一个长方形纸条折成的图形,已知图中∠2=122°,则∠1=116°.