题目内容
李栓身高1.92m，王鹏身高1.60m，他们在同一时刻站在阳光下，李栓的影子长为1.20m，求王鹏的影长．
考点：相似三角形的应用
专题：
分析：设王鹏的影长为h，根据同一时刻物高与影长成正比求出h的值即可．
解答：解：设王鹏的影长为h，
∵李栓身高1.92m，王鹏身高1.60m，他们在同一时刻站在阳光下，李栓的影子长为1.20m，
∴
=
，解得h=1.00（m）．
答：王鹏的影长是1.00米．
∵李栓身高1.92m，王鹏身高1.60m，他们在同一时刻站在阳光下，李栓的影子长为1.20m，
∴
| 1.92 |
| 1.20 |
| 1.60 |
| h |
答：王鹏的影长是1.00米．
点评：本题考查的是相似三角形的应用，熟知同一时刻物高与影长成正比是解答此题的关键．
练习册系列答案
期末复习检测系列答案
超能学典单元期中期末专题冲刺100分系列答案
黄冈360度定制密卷系列答案
阳光考场单元测试卷系列答案
相关题目
在平面直角坐标系中，某个图形经过了一定的变化，大小和形状都没有改变，这个图形上各点的坐标有可能做了一种变化，下列变化中，正确的是（ ）
| A、纵、横坐标分别乘以2 | ||
B、纵、横坐标分别变成原来的
| ||
| C、横坐标不变，纵坐标分别加2 | ||
| D、纵坐标不变，横坐标分别变成原来的2倍 |
如图，已知BE平分∠ABC，∠CBE=25°，∠BED=25°，∠C=30°，求∠ADE与∠BEC的度数．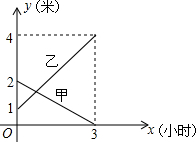
某企业有甲乙两个长方形的蓄水池，将甲池中的水注入乙池，甲乙两个蓄水池中水的深度y（m）与注水时间x（h）之间的函数图象如图，结合图象回答下列问题：