Question

（2013•宝应县二模）在直角三角形ABC中，∠ACB=90°，AC=6，BC=8，O为AB上一点，OA=

15

4

，以O为圆心，OA为半径作圆．
（1）试判断⊙O与BC的位置关系，并说明理由；
（2）若⊙O与AC交于点另一点D，求CD的长．

Answer 1

分析：（1）过点O作OE⊥BC，先根据勾股定理计算出AB=10，则OB=AB-OA=10-

15

4

=

25

4

，根据相似三角形的判定方法易得△BOE∽△BAC，则OE：AC=OB：AB，即OE：6=

25

4

：10，可计算得OE=

15

4

，由于圆的半径OA=

15

4

，根据切线的判定方法得到⊙O与BC相切；
（2）作OF⊥AC于F点，根据垂径定理得AF=DF，根据相似三角形的判定方法易得△AOF∽△ABC，则AF：AC=AO：AB，即AF：6=

15

4

：10，可计算得AF=

9

4

，则AD=2AF=

9

2

，然后理由CD=AC-AD进行计算即可．

解答：解：（1）⊙O与BC相切．理由如下：
过点O作OE⊥BC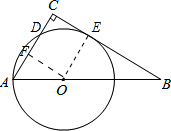，如图，
∵∠ACB=90°，AC=6，BC=8，
∴AB=

AC2+BC2

=10，
∴OB=AB-OA=10-

15

4

=

25

4

，
∵∠ACB=90°，
∴OE∥AC，
∴△BOE∽△BAC，
∴OE：AC=OB：AB，即OE：6=

25

4

：10，
∴OE=

15

4

，
∴OE=OA，
而OE⊥BC
∴⊙O与BC相切；

（2）作OF⊥AC于F点，则AF=DF，如图，
∵∠C=90°，
∴OF∥BC，
∴△AOF∽△ABC，
∴AF：AC=AO：AB，即AF：6=

15

4

：10，
∴AF=

9

4

，
∴AD=2AF=

9

2

，
∴CD=AC-AD=6-

9

2

=

3

2

．

点评：本题考查了圆的切线的判定：如果圆心到直线的距离等于圆的半径，那么这条直线为圆的切线．也考查了勾股定理、垂径定理以及相似三角形的判定与性质．