题目内容
14．如果把分式$\frac{x+y}{xy}$（x＞0，y＜0）中的x变为原来的2倍，y变为原来的一半，则分式的值（ ）| A． | 变大 | B． | 变小 | C． | 不变 | D． | 不确定 |
分析 根据分式的基本性质即可求出变换后的式子，然后用作差法即可判断．
解答 解：$\frac{2x+\frac{1}{2}y}{2x•\frac{1}{2}y}$=$\frac{4x+y}{2xy}$，
∴$\frac{x+y}{xy}$-$\frac{4x+y}{2xy}$=$\frac{-2x+y}{2xy}$
∵x＞0，y＜0，
∴-2x+y＜0，xy＜0，
∴$\frac{x+y}{xy}＞\frac{-2x+y}{2xy}$，
故选（B）
点评 本题考查分式的基本性质，解题的关键是求出变换的分式，本题属于中等题型．
练习册系列答案
阅读快车系列答案
相关题目
5．下列方程组是二元一次方程组的是（ ）
| A． | $\left\{\begin{array}{l}{x-y=1}\\{xy=2}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{\frac{1}{x}-1=y}\\{3x+y=0}\end{array}\right.$ | C． | $\left\{\begin{array}{l}{{x}^{2}-x-2=0}\\{y=x+1}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{4x-y=-1}\\{y=2x+3}\end{array}\right.$ |
19．
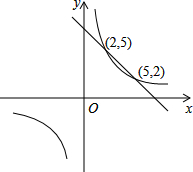已知，一次函数y1=ax+b与反比例函数y2=$\frac{k}{x}$的图象如图所示，当y1＜y2时，x的取值范围是（ ）
已知，一次函数y1=ax+b与反比例函数y2=$\frac{k}{x}$的图象如图所示，当y1＜y2时，x的取值范围是（ ）| A． | x＜2 | B． | 0＜x＜2或x＞5 | C． | 2＜x＜5 | D． | x＞5 |
3．下列各式利用完全平方公式计算正确的是（ ）
| A． | （x+3）2=x2+9 | B． | （-2a+b）2=4a2+4ab+b2 | ||
| C． | （a-2b）2=a2-2ab+4b2 | D． | （$\frac{1}{2}$-x）2=x2-x+$\frac{1}{4}$ |
4．下列二次根式中，与3$\sqrt{2}$是同类二次根式的是（ ）
| A． | $\sqrt{2}$ | B． | $\sqrt{24}$ | C． | $\sqrt{27}$ | D． | $\sqrt{50}$ |