题目内容
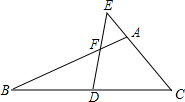 已知D为△ABC中BC边上的点,E为CA的延长线上一点,DE交AB于F,∠EAF=∠EDC,求证:
已知D为△ABC中BC边上的点,E为CA的延长线上一点,DE交AB于F,∠EAF=∠EDC,求证:| BD |
| BF |
| AF |
| EF |
考点:相似三角形的判定与性质
专题:证明题
分析:如图,作辅助线,证明△BGF∽△AEF,得到BF:GF=AF:EF;证明△BGF∽△DGB,得到BD:BF=BF:GF,即可解决问题.
解答: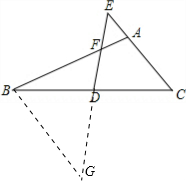 证明:如图,过点B作BG∥AC,交ED的延长线于点G;
证明:如图,过点B作BG∥AC,交ED的延长线于点G;
则△BGF∽△AEF,
∴BF:AF=GF:EF,
∴BF:GF=AF:EF;
∵BG∥AC,
∴∠EAF=∠BGF;
而∠EAF=∠EDC,∠BDG=∠EDC,
∴∠GBF=∠BDG,而∠G=∠G,
∴△BGF∽△DGB,
∴BD:BF=BG:GF,
∴BD:BF=AF:EF,
即
=
.
 证明:如图,过点B作BG∥AC,交ED的延长线于点G;
证明:如图,过点B作BG∥AC,交ED的延长线于点G;则△BGF∽△AEF,
∴BF:AF=GF:EF,
∴BF:GF=AF:EF;
∵BG∥AC,
∴∠EAF=∠BGF;
而∠EAF=∠EDC,∠BDG=∠EDC,
∴∠GBF=∠BDG,而∠G=∠G,
∴△BGF∽△DGB,
∴BD:BF=BG:GF,
∴BD:BF=AF:EF,
即
| BD |
| BF |
| AF |
| EF |
点评:该题主要考查了相似三角形的判定及其性质的应用问题;解题的关键是作辅助线,灵活运用有关定理来分析、判断、推理或解答;对综合的分析问题解决问题的能力提出了较高的要求.

练习册系列答案
相关题目

 如图,在菱形ABCD中,对角线AC与BD相交于点O,OE⊥AB,垂足为E,若∠ADC=130°,则∠AOE的大小为
如图,在菱形ABCD中,对角线AC与BD相交于点O,OE⊥AB,垂足为E,若∠ADC=130°,则∠AOE的大小为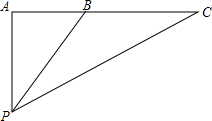 为制作一部海洋专题片,一摄像师在一直升飞机上进行航拍,飞机在同一高度沿一条直线飞行,飞机每秒钟飞行20米.当飞机飞到A点时,摄像师发现自己的正下方的海面上有一美丽景色P,一段时间后飞机飞到B点,此时测得其俯角是35.1°,又经过了半分钟,飞机飞到C点,此时测得此俯角是16.8°,由此你能知道飞机的大约高度吗?(参考数据:sin35.1°=0.58,cos35.1°=0.82,tan35.1°=0.70,sin16.8°=0.29,cos16.8°=0.96,tan16.8°=0.30)
为制作一部海洋专题片,一摄像师在一直升飞机上进行航拍,飞机在同一高度沿一条直线飞行,飞机每秒钟飞行20米.当飞机飞到A点时,摄像师发现自己的正下方的海面上有一美丽景色P,一段时间后飞机飞到B点,此时测得其俯角是35.1°,又经过了半分钟,飞机飞到C点,此时测得此俯角是16.8°,由此你能知道飞机的大约高度吗?(参考数据:sin35.1°=0.58,cos35.1°=0.82,tan35.1°=0.70,sin16.8°=0.29,cos16.8°=0.96,tan16.8°=0.30)