题目内容
11.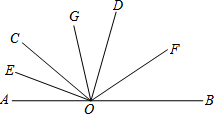 如图,∠AOC:∠COD:∠BOD=2:3:4,且A,O,B三点在一条直线上,OE,OF分别平分∠AOC和∠BOD,OG平分∠EOF,求∠GOF的度数.将下列解题过程补充完整.
如图,∠AOC:∠COD:∠BOD=2:3:4,且A,O,B三点在一条直线上,OE,OF分别平分∠AOC和∠BOD,OG平分∠EOF,求∠GOF的度数.将下列解题过程补充完整.解:因为,∠AOC:∠COD:∠BOD=2:3:4,所以∠AOC=40°,∠COD=60°,∠BOD=80°,因为OE,OF分别平分∠AOC和∠BOD,所以∠AOE=20°,∠BOF=40°,所以∠EOF=120°,
又因为OG平分∠EOF,所以∠GOF=60°.
分析 根据互补两角的和为180°和角平分线的性质即可求得∠EOF的大小,即可解题.
解答 解:∵∠AOC:∠COD:∠BOD=2:3:4,∠AOC+∠COD+∠BOD=180°,
∴∠AOC=40°,∠COD=60°,∠BOD=80°,
∵OE、OF分别平分∠AOC和∠BOD,
∴∠AOE=∠COE=20°,∠BOF=∠DOF=40°,
∴∠EOF=180°-20°-40°=120°,
∵OG平分∠EOF,
∴∠GOF=60°,
故答案为:40°,60°,80°,20°,40°,120°,OG平分∠EOF.
点评 本题考查了补角的性质、角平分线平分角的性质,求得∠EOF是解题的关键.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
1.下列单项式系数相同的是( )
①2x2 ②-2y2 ③$\frac{1}{2}$x2 ④2x3y4z.
①2x2 ②-2y2 ③$\frac{1}{2}$x2 ④2x3y4z.
| A. | ①② | B. | ②③ | C. | ①④ | D. | ①③ |
20.一元二次方程5x2-3x+1=0的一次项系数是( )
| A. | -3 | B. | 3 | C. | 5 | D. | -3x |
 已知:P是边长为4厘米的正方形ABCD的边BC上的点,且PC=1厘米,M是CD边上的一个动点,
已知:P是边长为4厘米的正方形ABCD的边BC上的点,且PC=1厘米,M是CD边上的一个动点, 如图,放置的一个机器零件(图1),若从正面看到的图形如(图2)所示,则从上面看到的图形是( )
如图,放置的一个机器零件(图1),若从正面看到的图形如(图2)所示,则从上面看到的图形是( )



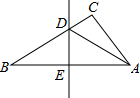 如图,在△ABC中,边AB的垂直平分线分别交BC、AB于点D、E,△ADC的周长为9cm,△ABC的周长为13cm,则AE=2cm.
如图,在△ABC中,边AB的垂直平分线分别交BC、AB于点D、E,△ADC的周长为9cm,△ABC的周长为13cm,则AE=2cm.