题目内容
已知凸四边形ABCD中,∠A=∠C=90°.
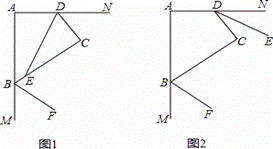
(1)如图1,若DE平分∠ADC,BF平分∠ABC的邻补角,判断DE与BF位置关系并证明;
(2)如图2,若BF、DE分别平分∠ABC、∠ADC的邻补角,判断DE与BF位置关系并证明。
(1)解:延长DE交BF于点G………(1分)
∵∠A+∠ABC+∠C+∠ADC=360°
又∵∠A=∠C=90°,
∴∠ABC+∠ADC=180°
∵∠ABC+∠MBC=180°
∴∠ADC=∠MBC…………(2分)
 ∵DE、BF分别平分∠ADC、∠MBC
∵DE、BF分别平分∠ADC、∠MBC
∴∠EDC=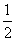 ∠ADC,∠EBG=
∠ADC,∠EBG=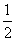 ∠MBC,(3分)
∠MBC,(3分)
∴∠EDC=∠EBG…………(4分)
∵∠EDC+∠DEC+∠C=180°
∠EBG+∠BEG+∠EGB=180°
又∵∠DEC=∠BEG ∴∠EGB=∠C=90
∴ DE⊥BF……………(5分)
(2)解:连接BD…… …………(6分)
…………(6分)
∵DE、BF分别平分∠NDC、∠MBC
∴∠EDC=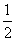 ∠NDC,∠FBC=
∠NDC,∠FBC=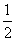 ∠MBC,(7分)
∠MBC,(7分)
∵∠ADC+∠NDC=180°
又∵∠ADC=∠MBC
∴∠MBC+∠NDC=180°
∴∠EDC+∠FBC= 90°………………(8分)
90°………………(8分)
∵∠C=90° ∴∠CDB+∠CBD=90°
 ∴∠EDC+∠CDB +∠FBC +∠CBD=180°
∴∠EDC+∠CDB +∠FBC +∠CBD=180°
即∠EDB+∠FBD=180°……………(9分)
∴ D E∥BF……………(10分)
E∥BF……………(10分)

练习册系列答案
相关题目
 的负数: .
的负数: . 系中,四边形ABCD是梯形,AD∥BC,
系中,四边形ABCD是梯形,AD∥BC, 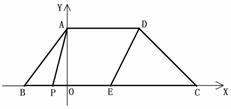 在⑴的条件下,点P在BC边上运动过程中,以点P、A、D、E为顶点的四边形能否
在⑴的条件下,点P在BC边上运动过程中,以点P、A、D、E为顶点的四边形能否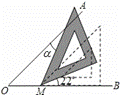
 ,求代数式
,求代数式
 中,函数值
中,函数值 随
随 的增大而 .
的增大而 . 部分折成一个无盖的长方体盒子.
部分折成一个无盖的长方体盒子.