题目内容
5.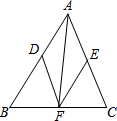 △ABC中,DF∥AC,EF∥AB,AF平分∠BAC.
△ABC中,DF∥AC,EF∥AB,AF平分∠BAC.(1)你能判断四边形ADFE是菱形吗?并说明理由.
(2)∠BAC满足什么条件时,四边形ADFE是正方形?并说明理由.
分析 (1)由已知易得四边形ADFE是平行四边形,由角平分线定义和平行线的性质可得∠FAD=∠DFA,则DF=DA,从而证明四边形ADFE是菱形;
(2)由(1)已经证明四边形ADFE是菱形,又根据有一个角为直角的菱形是正方形,可得当△ABC是直角三角形时,四边形ADFE是正方形.
解答  解:(1)能.理由如下:
解:(1)能.理由如下:
∵DF∥AC,EF∥AB,
∴四边形ADFE是平行四边形;
∵AF平分∠BAC,
∴∠EAF=∠FAD,
∵AE∥DF,
∴∠EAF=∠DFA,
∴∠FAD=∠DFA,
∴DF=DA,
∴四边形ADFE是菱形;
(2)当∠BAC=90°时,四边形AEDF是正方形;
∵四边形AEDF是菱形,∠BAC=90°,
∴四边形AEDF是正方形.
点评 此题主要考查了菱形和正方形的判定,关键是掌握一组邻边相等的平行四边形是菱形,有一个角为直角的菱形是正方形.

练习册系列答案
相关题目
15. 如图,平行四边形ABCD中,对角线AC,BD相交于O,AC=8,BD=10,则边AB的取值范围是( )
如图,平行四边形ABCD中,对角线AC,BD相交于O,AC=8,BD=10,则边AB的取值范围是( )
 如图,平行四边形ABCD中,对角线AC,BD相交于O,AC=8,BD=10,则边AB的取值范围是( )
如图,平行四边形ABCD中,对角线AC,BD相交于O,AC=8,BD=10,则边AB的取值范围是( )| A. | 8<AB<10 | B. | 1<AB<9 | C. | 4<AB<5 | D. | 2<AB<18 |
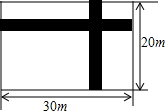 在宽为20米、长为30米的矩形地面上修建两条同样宽的道路,余下部分作为耕地.若耕地面积需要551米2,则修建的路宽应为多少?
在宽为20米、长为30米的矩形地面上修建两条同样宽的道路,余下部分作为耕地.若耕地面积需要551米2,则修建的路宽应为多少? 如图,AD⊥BC,BD=DC,点C在AE的垂直平分线上,AB、AC、CE的长度有什么关系?AB=AC=CE,AB+BD与DE有什么关系?AB+BD=DE.
如图,AD⊥BC,BD=DC,点C在AE的垂直平分线上,AB、AC、CE的长度有什么关系?AB=AC=CE,AB+BD与DE有什么关系?AB+BD=DE.