题目内容
计算题
(1)(n2)3•(n4)2
(2)(-6a2b5c)÷(-2ab2)2
(3)(8a3b-5a2b2)÷4ab
(4)(-2a2)(3ab2-5ab3).
(5)(3y+2)(y-4)-3(y-2)(y-3)
(6)(2x+y)2-(2x+3y)(2x-3y)
(7)(x+2y-3)(x-2y+3)
(8)(2x3y)2•(-2xy)+(-2x3y)3÷(2x2)
(9)(x+3)(x-3)(x2-9)
(1)(n2)3•(n4)2
(2)(-6a2b5c)÷(-2ab2)2
(3)(8a3b-5a2b2)÷4ab
(4)(-2a2)(3ab2-5ab3).
(5)(3y+2)(y-4)-3(y-2)(y-3)
(6)(2x+y)2-(2x+3y)(2x-3y)
(7)(x+2y-3)(x-2y+3)
(8)(2x3y)2•(-2xy)+(-2x3y)3÷(2x2)
(9)(x+3)(x-3)(x2-9)
考点:整式的混合运算
专题:计算题
分析:(1)原式利用幂的乘方与积的乘方运算法则计算,再利用同底数幂的乘法法则计算即可;
(2)原式先计算乘方运算,再计算除法运算即可;
(3)原式利用多项式除以单项式法则计算即可;
(4)原式利用单项式乘以多项式法则计算即可;
(5)原式利用多项式乘以多项式法则计算,去括号合并即可;
(6)原式第一项利用完全平方公式展开,第二项利用平方差公式化简,去括号合并即可;
(7)原式利用平方差公式化简,再利用完全平方公式展开即可;
(8)原式先计算乘方运算,再计算乘除运算,最后算加减运算即可;
(9)原式利用平方差公式计算即可得到结果.
(2)原式先计算乘方运算,再计算除法运算即可;
(3)原式利用多项式除以单项式法则计算即可;
(4)原式利用单项式乘以多项式法则计算即可;
(5)原式利用多项式乘以多项式法则计算,去括号合并即可;
(6)原式第一项利用完全平方公式展开,第二项利用平方差公式化简,去括号合并即可;
(7)原式利用平方差公式化简,再利用完全平方公式展开即可;
(8)原式先计算乘方运算,再计算乘除运算,最后算加减运算即可;
(9)原式利用平方差公式计算即可得到结果.
解答:解:(1)(n2)3•(n4)2=n6•n8=n14;
(2)(-6a2b5c)÷(-2ab2)2=(-6a2b5c)÷(4a2b4)=-
bc;
(3)(8a3b-5a2b2)÷4ab=2a2-
ab;
(4)(-2a2)(3ab2-5ab3)=-6a3b2+10a3b3;
(5)(3y+2)(y-4)-3(y-2)(y-3)=3y2-12y+2y-8-3y2+15y-18=5y-26;
(6)(2x+y)2-(2x+3y)(2x-3y)=4x2+4xy+y2-4x2+9y2=4xy+10y2;
(7)(x+2y-3)(x-2y+3)=x2-(2y-3)2=x2-4y2+12y-9;
(8)(2x3y)2•(-2xy)+(-2x3y)3÷(2x2)=-8x7y3-4x7y3=-12x7y3;
(9)(x+3)(x-3)(x2-9)=(x2+9)(x2-9)=x4-81.
(2)(-6a2b5c)÷(-2ab2)2=(-6a2b5c)÷(4a2b4)=-
| 3 |
| 2 |
(3)(8a3b-5a2b2)÷4ab=2a2-
| 5 |
| 4 |
(4)(-2a2)(3ab2-5ab3)=-6a3b2+10a3b3;
(5)(3y+2)(y-4)-3(y-2)(y-3)=3y2-12y+2y-8-3y2+15y-18=5y-26;
(6)(2x+y)2-(2x+3y)(2x-3y)=4x2+4xy+y2-4x2+9y2=4xy+10y2;
(7)(x+2y-3)(x-2y+3)=x2-(2y-3)2=x2-4y2+12y-9;
(8)(2x3y)2•(-2xy)+(-2x3y)3÷(2x2)=-8x7y3-4x7y3=-12x7y3;
(9)(x+3)(x-3)(x2-9)=(x2+9)(x2-9)=x4-81.
点评:此题考查了整式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案
相关题目
下列说法中正确的是( )
| A、61550 保留两个有效数字为6.1×104 |
| B、近似数2.30×10-1有3个有效数字,精确到了百分位 |
| C、近似数15.04万有4个有效数字,精确到了百位 |
| D、4.6502精确到0.001为4.65,有3个有效数字 |
在下列代数式中,次数为3的单项式是( )
| A、xy |
| B、x3-y3 |
| C、x2y |
| D、3xy |
 请从以下两个小题中任选一个作答,若多选,则按所选的第一题计分.
请从以下两个小题中任选一个作答,若多选,则按所选的第一题计分.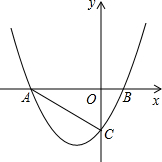 已知:二次函数y=
已知:二次函数y=