题目内容
已知：如图，AB、DE是⊙O的直径，AC∥DE，交⊙O于点C，求证：BE=CE．考点：圆心角、弧、弦的关系
专题：证明题
分析：连接OC，由AC∥DE可知∠1=∠A，∠2=∠3，再根据∠A=∠3可得出∠1=∠2，故可得出结论．
解答：
证明：连接OC，
∵AC∥DE，
∴∠1=∠A，∠2=∠3，
∵∠A=∠3，
∴∠1=∠2，
∴BE=CE．
证明：连接OC，∵AC∥DE，
∴∠1=∠A，∠2=∠3，
∵∠A=∠3，
∴∠1=∠2，
∴BE=CE．
点评：本题考查的是圆心角、弧、弦的关系，熟知在同圆和等圆中，相等的圆心角所对的弧相等，所对的弦也相等是解答此题的关键．
练习册系列答案
七彩题卡口算应用一点通系列答案
相关题目
不解方程，判别2x2-x-1=0的根的情况是（ ）
| A、方程有两个不相等的实数根 |
| B、方程有两个相等的实数根 |
| C、方程无实数根 |
| D、方程有一个实数根 |
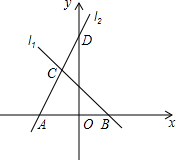如图，直线l1的解析式为y=-x+2，l1与x轴交于点B，直线l2经过点D（0，5），与直线l1交于点C（-1，m），且与x轴交于点A
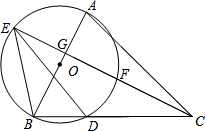如图，在△ABC中，以AB边为直径的⊙O交BC于点D，CE⊥AB分别交⊙O于点E、F两点，交AB于点G，连接BE、DE．