题目内容
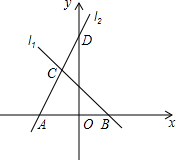 如图,直线l1的解析式为y=-x+2,l1与x轴交于点B,直线l2经过点D(0,5),与直线l1交于点C(-1,m),且与x轴交于点A
如图,直线l1的解析式为y=-x+2,l1与x轴交于点B,直线l2经过点D(0,5),与直线l1交于点C(-1,m),且与x轴交于点A(1)求点C的坐标及直线l2的解析式;
(2)求△ABC的面积.
考点:两条直线相交或平行问题
专题:
分析:(1)首先利用待定系数法求出C点坐标,然后再根据D、C两点坐标求出直线l2的解析式;
(2)首先根据两个函数解析式计算出A、B两点坐标,然后再利用三角形的面积公式计算出△ABC的面积即可.
(2)首先根据两个函数解析式计算出A、B两点坐标,然后再利用三角形的面积公式计算出△ABC的面积即可.
解答:解:(1)∵直线l1的解析式为y=-x+2经过点C(-1,m),
∴m=1+2=3,
∴C(-1,3),
设直线l2的解析式为y=kx+b,
∵经过点D(0,5),C(-1,3),
∴
,
解得
,
∴直线l2的解析式为y=2x+5;
(2)当y=0时,2x+5=0,
解得x=-
,
则A(-
,0),
当y=0时,-x+2=0
解得x=2,
则B(2,0),
△ABC的面积:
×(2+
)×3=
.
∴m=1+2=3,
∴C(-1,3),
设直线l2的解析式为y=kx+b,
∵经过点D(0,5),C(-1,3),
∴
|
解得
|
∴直线l2的解析式为y=2x+5;
(2)当y=0时,2x+5=0,
解得x=-
| 5 |
| 2 |
则A(-
| 5 |
| 2 |
当y=0时,-x+2=0
解得x=2,
则B(2,0),
△ABC的面积:
| 1 |
| 2 |
| 5 |
| 2 |
| 27 |
| 4 |
点评:此题主要考查了待定系数法求一次函数解析式,关键是掌握凡是函数图象经过的点必能满足解析式.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
下列说法中正确的是( )
| A、钝角三角形有三条高线都在三角形外部 |
| B、三角形的一个外角大于任何一个内角 |
| C、与三角形三个顶点的距离相等的点是三条角平分线的交点 |
| D、若点P(2,a)和点Q(b,-3)关于x轴对称,则a+b的值为5 |
 如图,矩形ABCD的对角线AC、BD相交于点O,CE∥BD,DE∥AC,若AC=5,则四边形CODE的周长是( )
如图,矩形ABCD的对角线AC、BD相交于点O,CE∥BD,DE∥AC,若AC=5,则四边形CODE的周长是( ) 如图,已知△ABE,AB、AE边上的垂直平分线m1、m2交BE分别为点C、D,且BC=CD=DE,求∠BAE的度数.
如图,已知△ABE,AB、AE边上的垂直平分线m1、m2交BE分别为点C、D,且BC=CD=DE,求∠BAE的度数. 已知:如图,AB、DE是⊙O的直径,AC∥DE,交⊙O于点C,求证:BE=CE.
已知:如图,AB、DE是⊙O的直径,AC∥DE,交⊙O于点C,求证:BE=CE.