题目内容
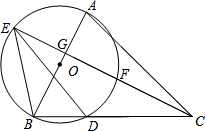 如图,在△ABC中,以AB边为直径的⊙O交BC于点D,CE⊥AB分别交⊙O于点E、F两点,交AB于点G,连接BE、DE.
如图,在△ABC中,以AB边为直径的⊙O交BC于点D,CE⊥AB分别交⊙O于点E、F两点,交AB于点G,连接BE、DE.(1)求证:∠BED=∠BCE;
(2)若∠ACB=45°,AB=
| 5 |
考点:相似三角形的判定与性质,圆周角定理
专题:
分析:(1)连接AD,得出∠BED=∠BAD,根据三角形内角和定理求出∠BAD=∠BCE,即可得出答案.
(2)连接AE,求出AD=DC=2,在Rt△ADB中,由勾股定理求出BD=1,证△BED∽△BCE,得出
=
,求出BE,由勾股定理求出AE=
,在△AEB中,根据三角形面积公式得出AE×BE=AB×EG,求出EG,根据垂径定理求出EF即可.
(2)连接AE,求出AD=DC=2,在Rt△ADB中,由勾股定理求出BD=1,证△BED∽△BCE,得出
| BE |
| BD |
| BC |
| BE |
| 2 |
解答:(1)证明: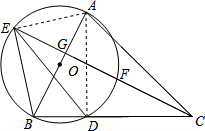
连接AD,
则∠BED=∠BAD,
∵CE⊥AB,
∴∠CGB=90°,
∴∠ABD+∠BCE=90°,
∵AB为直径,
∴∠ADB=90°,
∴∠ABD+∠BAD=90°,
∴∠BAD=∠BCE,
∴∠BED=∠BCE.
(2)解:连接AE,
∵∠ADC=90°,∠ACB=45°,
∴∠DAC=∠ACB=45°,
∴AD=DC=2,
∴在Rt△ADB中,由勾股定理得:BD=
=1,
∵∠EBD=∠EBD,∠BED=∠BCE,
∴△BED∽△BCE,
∴
=
,
∴BE2=1×(1+2)=3,
∴BE=
,
∵AB是直径,
∴∠AEB=90°,由勾股定理得:AE=
=
=
,
在△AEB中,根据三角形面积公式得:AE×BE=AB×EG,
×
=
EG,
EG=
,
∵AB⊥EF,AB过O,
∴EF=2EG=
.

连接AD,
则∠BED=∠BAD,
∵CE⊥AB,
∴∠CGB=90°,
∴∠ABD+∠BCE=90°,
∵AB为直径,
∴∠ADB=90°,
∴∠ABD+∠BAD=90°,
∴∠BAD=∠BCE,
∴∠BED=∠BCE.
(2)解:连接AE,
∵∠ADC=90°,∠ACB=45°,
∴∠DAC=∠ACB=45°,
∴AD=DC=2,
∴在Rt△ADB中,由勾股定理得:BD=
(
|
∵∠EBD=∠EBD,∠BED=∠BCE,
∴△BED∽△BCE,
∴
| BE |
| BD |
| BC |
| BE |
∴BE2=1×(1+2)=3,
∴BE=
| 3 |
∵AB是直径,
∴∠AEB=90°,由勾股定理得:AE=
| AB2-BE2 |
(
|
| 2 |
在△AEB中,根据三角形面积公式得:AE×BE=AB×EG,
| 2 |
| 3 |
| 5 |
EG=
| ||
| 5 |
∵AB⊥EF,AB过O,
∴EF=2EG=
2
| ||
| 5 |
点评:本题考查了相似三角形的性质和判定,勾股定理,三角形面积,圆周角定理,垂径定理等知识点的应用,主要考查学生综合运用定理进行推理和计算的能力.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
方程x(x+1)=2(x+1)的解是( )
| A、2 | B、-1 |
| C、-1或2 | D、1或2 |
在函数y=
(a为常数)的图象上有三点(-1,y1),(-
,y2),(
,y3),则函数值y1、y2、y3的大小关系是( )
| -a2-1 |
| x |
| 1 |
| 4 |
| 1 |
| 2 |
| A、y2<y3<y1 |
| B、y3<y2<y1 |
| C、y1<y2<y3 |
| D、y3<y1<y2 |
 如图,已知△ABE,AB、AE边上的垂直平分线m1、m2交BE分别为点C、D,且BC=CD=DE,求∠BAE的度数.
如图,已知△ABE,AB、AE边上的垂直平分线m1、m2交BE分别为点C、D,且BC=CD=DE,求∠BAE的度数. 已知:如图,AB、DE是⊙O的直径,AC∥DE,交⊙O于点C,求证:BE=CE.
已知:如图,AB、DE是⊙O的直径,AC∥DE,交⊙O于点C,求证:BE=CE. 在一条笔直的河道上依次有A,B,C,三个港口在一条直线上依次有A、B、C三个港口,甲、乙两船同时分别从A、B港口出发,沿直线匀速驶向C港,最终达到C港.设甲、乙两船行驶x(h)后,与B港的距离分别为y1、y2(km),y1、y2与x的函数关系如图.
在一条笔直的河道上依次有A,B,C,三个港口在一条直线上依次有A、B、C三个港口,甲、乙两船同时分别从A、B港口出发,沿直线匀速驶向C港,最终达到C港.设甲、乙两船行驶x(h)后,与B港的距离分别为y1、y2(km),y1、y2与x的函数关系如图.