题目内容
已知两圆的半径R,r分别为方程x2-7x+12=0的两根,两圆的圆心距为1,两圆的位置关系是( )
| A、外离 | B、内切 | C、相交 | D、外切 |
考点:圆与圆的位置关系,解一元二次方程-因式分解法
专题:
分析:本题可先求出方程的根即两圆的半径R、r,再根据由数量关系来判断两圆位置关系的方法,确定两圆的位置关系.设两圆圆心距为P,两圆半径分别为R和r,且R≥r,则有:外离P>R+r;外切P=R+r;相交R-r<P<R+r;内切P=R-r;内含P<R-r.
解答:解:∵两圆的半径分别是方程x2-7x+12=0的两根,
∴(x-3)(x-4)=0,
解得:x=3或x=4,
∴R-r=1,
即圆心距等于半径差,
∴根据圆心距与半径之间的数量关系可知⊙O1与⊙O2的位置关系是内切.
故选B.
∴(x-3)(x-4)=0,
解得:x=3或x=4,
∴R-r=1,
即圆心距等于半径差,
∴根据圆心距与半径之间的数量关系可知⊙O1与⊙O2的位置关系是内切.
故选B.
点评:本题考查了解一元二次方程和由数量关系来判断两圆位置关系的方法.注意此类题型可直接求出解判断,也可利用根与系数的关系找到两个根的差或和.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
不等式组
的解集在数轴上表示正确的是( )
|
A、 |
B、 |
C、 |
D、 |
根据不等式的性质,下列变形正确的是( )
| A、由-a<1得a<-1 | ||||
B、由-2a>-1得a<
| ||||
C、由-
| ||||
D、由-
|
不等式组
的解集在数轴上表示,正确的是( )
|
A、 |
B、 |
C、 |
D、 |
下列各式中①
;②
; ③
; ④
; ⑤b+
=3;⑥
一定是二次根式的有( )个.
| a |
| b+1 |
| a2 |
| a2+3 |
| b2-6b+9 |
| x2+2x+1 |
| A、1 个 | B、2个 |
| C、3个 | D、4个 |
 如图,已知,∠A=42°,∠D=138°,BP、CP分别平分∠ABD、∠ACD.求证:BP⊥CP.
如图,已知,∠A=42°,∠D=138°,BP、CP分别平分∠ABD、∠ACD.求证:BP⊥CP.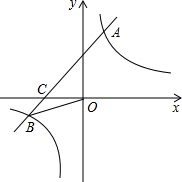 已知:如图,在平面直角坐标系中,一次函数y1=ax+b(a≠0)的图象与反比例函数
已知:如图,在平面直角坐标系中,一次函数y1=ax+b(a≠0)的图象与反比例函数