题目内容
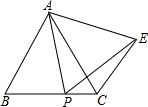
如图,△ABC是等边三角形,P为BC上一动点(不与B、C重合),以AP为边作等边△APE,连接CE.
(1)求证:AB∥CE;
(2)是否存在点P,使得AE⊥CE?若存在,指出点P的位置并证明你的结论;若不存,请说明理由.

【考点】全等三角 形的判定与性质;等边三角形的性质.
形的判定与性质;等边三角形的性质.
【分析】(1)根据等边三角形的性质得出角相等、边相等,证出△A BP≌△ACE(SAS),得出对应角相等,证出∠BAC=∠ACF,从而证出结论.
BP≌△ACE(SAS),得出对应角相等,证出∠BAC=∠ACF,从而证出结论.
(2)由△ABP≌△ACE得出∠APB=∠AEC=90°,再由等边三角形的性质得出P为BC的中点.
【解答】证明:(1)∵△ABC、△APE是等边三角形,
∴∠BAC=∠PAE=∠B=60°,AB=AC,AF=AE,
∴∠BAP=∠CAE,
在△ABF和△ACE中,
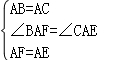
∴△ABP≌△ACE(SAS),
∴∠B=∠ACP=60°,
∴∠BAC=∠ACF,
∴AB∥CE;
(2)存在点P使得AE⊥CE.此时P为BC的中点;理由如下:
∵AE⊥CE,
∴∠AEC=90°,
由(1)得:△ABP≌△A CE,
CE,
∴∠APB=∠AEC=90°,
∴AP⊥BC,
∵AB=AC,
∴P为BC的中点.
∴存在点P,使得AE⊥CE.
【点评】本题考查了等边三角形的性质以及全等三角形的判定与性质;由等边三角形证明三角形全等是关键.

练习册系列答案
相关题目
 =0的根的情况为( )
=0的根的情况为( ) 和点D、E、F、G、H、K均在格点上,现以D、E、F、G、H、K中的三个点为顶点画三角形.
和点D、E、F、G、H、K均在格点上,现以D、E、F、G、H、K中的三个点为顶点画三角形.
 (x﹣1)2+4,若y随x的增大而减小,则x的取值范围是( )
(x﹣1)2+4,若y随x的增大而减小,则x的取值范围是( )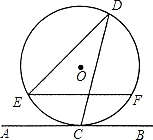
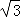 C.
C.
