题目内容
有人说，无论x取何实数，代数式x2+y2-6x-8y+25的值总是非负数．你的看法如何？请谈谈你的理由．
考点：配方法的应用,非负数的性质：偶次方
专题：
分析：先把原代数式利用配方法转化为x2+y2-6x-8y+25=（x-3）2+（y-4）2的形式，然后根据非负数的性质来讨论代数式x2+y2-6x-8y+25的值的正负．
解答：解：无论x取何实数，代数式x2+y2-6x-8y+25的值总是非负数．理由如下：
x2+y2-6x-8y+25=（x-3）2+（y-4）2；
∵无论x，y取何值，（x-3）2≥0，（y-4）2≥0，
∴x2+y2-6x-8y+25≥0．
因此代数式的值总是非负数．
x2+y2-6x-8y+25=（x-3）2+（y-4）2；
∵无论x，y取何值，（x-3）2≥0，（y-4）2≥0，
∴x2+y2-6x-8y+25≥0．
因此代数式的值总是非负数．
点评：本题考查了配方法的应用、非负数的性质--偶次方．解题时要注意配方法的步骤．注意在变形的过程中不要改变式子的值．
练习册系列答案
相关题目
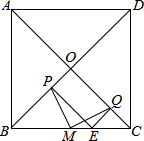如图所示，在正方形ABCD中，对角线AC，BD交于点O，M是BC的中点，E是BC上任意一点，EP⊥BD于点P，EQ⊥AC于点Q，连接MP和MQ，试说明MP=MQ．
如图⊙O中，AB，AC是弦，O在∠BAC的内部，∠ABO=α，∠ACO=β，∠BOC=γ，则α，β，γ的关系是什么？