题目内容
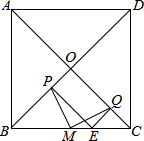 如图所示,在正方形ABCD中,对角线AC,BD交于点O,M是BC的中点,E是BC上任意一点,EP⊥BD于点P,EQ⊥AC于点Q,连接MP和MQ,试说明MP=MQ.
如图所示,在正方形ABCD中,对角线AC,BD交于点O,M是BC的中点,E是BC上任意一点,EP⊥BD于点P,EQ⊥AC于点Q,连接MP和MQ,试说明MP=MQ.考点:全等三角形的判定与性质,正方形的性质
专题:证明题
分析:连接OM,求出∠PBM=∠QOM,OM=BM,OQ=PE=PB,证明△OPM≌△QCM,根据全等三角形的性质得出即可.
解答:解:
连接OM,
∵四边形ABCD是正方形,
∴OB=OC,∠BOC=90°,
∵M为BC的中点,
∴OM=BM=CM,∠OBC=○OCB=45°=∠COM=∠BOM,∠OMB=90°,
∵∠BOC=90°,EQ⊥OC,EP⊥OB,
∴∠QOP=∠OPE=∠OQE=90°,
∴四边形OPEQ是矩形,
∴OQ=PE,∠OPE=90°,
∴∠BPE=90°,
∵∠PBC=45°,
∴∠PBE=∠PEB=45°,
∴BP=PE=OQ,
在△PBM和△QOM中
∴△PBM≌△QOM,
∴MP=MQ.

连接OM,
∵四边形ABCD是正方形,
∴OB=OC,∠BOC=90°,
∵M为BC的中点,
∴OM=BM=CM,∠OBC=○OCB=45°=∠COM=∠BOM,∠OMB=90°,
∵∠BOC=90°,EQ⊥OC,EP⊥OB,
∴∠QOP=∠OPE=∠OQE=90°,
∴四边形OPEQ是矩形,
∴OQ=PE,∠OPE=90°,
∴∠BPE=90°,
∵∠PBC=45°,
∴∠PBE=∠PEB=45°,
∴BP=PE=OQ,
在△PBM和△QOM中
|
∴△PBM≌△QOM,
∴MP=MQ.
点评:本题考查了正方形的性质,直角三角形的性质,全等三角形的性质和判定的应用,主要考查学生的推理能力,题目综合性比较强,有一定的难度.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目