题目内容
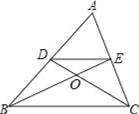
如图，在△ABC中两条中线BE、CD相交于点O，记△DOE的面积为S1，△COB的面积为S2，则S1：S2=（ ）
A．1：4 B．2：3 C．1：3 D．1：2
A【考点】相似三角形的判定与性质；三角形的重心．
【分析】根据三角形的中位线得出DE∥BC，DE=
BC，根据平行线的性质得出相似，根据相似三角形的性质求出即可．
【解答】解：∵BE和CD是△ABC的中线，
∴DE=
BC，DE∥BC，
∴
=，△DOE∽△COB，
∴
=（）2=（）2=
，
故选：A．
【点评】本题考查了相似三角形的性质和判定，三角形的中位线的应用，注意：相似三角形的面积比等于相似比的平方，三角形的中位线平行于第三边，并且等于第三边的一半．
练习册系列答案
相关题目
|+（cosB﹣
+
=2； 
，连接AB，过AB中点C1分别作x轴和y轴的垂线，垂足分别是点A1、B1，连接A1B1，再过A1B1中点C2作x轴和y轴的垂线，照此规律依次作下去，则点Cn的坐标为 ．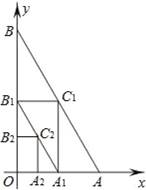
，则2xy的值为( )
D．
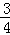，求线段CD的长．