Question

1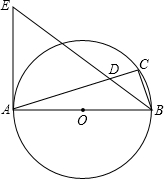．如图，AB是⊙O的直径，点C在⊙O上，∠ABC的平分线与AC相交于点D，与⊙O过点A的切线相交于点E．
（1）求证：AD=AE；
（2）若AB=8，AD=6，求BD．

Answer 1

分析 （1）利用角平分线和∠C=∠BAE=90°，得出∠E=∠4，从而得到AD=AE；
（2）先证明△BCD∽△BAE，利用相似比得到得出即$\frac{CD}{CB}=\frac{AE}{AB}=\frac{6}{8}$=$\frac{3}{4}$，若设CD=3x，则BC=4x，BD=5x，再利用勾股定理得到（4x）²+（6+3x）²=8²，然后解方程求出x后计算5x即可．

解答 解：（1）∵BE平分∠ABC，
∴∠1=∠2，
∵AB为直径，
∴∠C=90°，
∴∠2+∠3=90°，
∵AE为切线，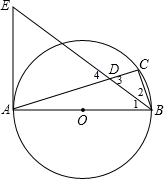
∴AE⊥AB，
∴∠E+∠1=90°，
∴∠E=∠3，
而∠4=∠3，
∴∠E=∠4，
∴AE=AD；

（2）解：∵∠2=∠1，
∴Rt△BCD∽Rt△BAE，
∴CD：AE=BC：AB，
即$\frac{CD}{CB}=\frac{AE}{AB}=\frac{6}{8}$=$\frac{3}{4}$，
设CD=3x，BC=4x，则BD=5x，
在Rt△ABC中，AC=AD+CD=3x+6，
∵（4x）²+（6+3x）²=8²，解得x₁=$\frac{14}{25}$，x₂=-2（舍去），
∴BD=5x=2.8．

点评 本题考查了切线的性质：圆的切线垂直于经过切点的半径；也考查了利用勾股定理和相似比进行几何计算．