题目内容
 如图所示,在Rt△ABC中,∠BAC=90°,AB=AC,E、D分别是BC、AC上的点,且∠AED=45°,求证:△ABE∽△ECD.
如图所示,在Rt△ABC中,∠BAC=90°,AB=AC,E、D分别是BC、AC上的点,且∠AED=45°,求证:△ABE∽△ECD.考点:相似三角形的判定
专题:证明题
分析:由∠BAC=90°,AB=AC得到∠B=∠C=45°,再根据三角形外角性质得∠AED+∠CED=∠B+∠BAE,加上∠AED=45°,则∠BAE=∠CED,于是可根据有两组角对应相等的两个三角形相似得到结论.
解答:证明:∵∠BAC=90°,AB=AC,
∴∠B=∠C=45°,
∵∠AEC=∠B+∠BAE,
即∠AED+∠CED=∠B+∠BAE,
∵∠AED=45°,
∴∠BAE=∠CED,
∴△ABE∽△ECD.
∴∠B=∠C=45°,
∵∠AEC=∠B+∠BAE,
即∠AED+∠CED=∠B+∠BAE,
∵∠AED=45°,
∴∠BAE=∠CED,
∴△ABE∽△ECD.
点评:本题考查了三角形相似的判定:有两组角对应相等的两个三角形相似.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列说法不正确的是( )
A、
| ||||
| B、-9是81的算术平方根 | ||||
| C、(-0.1)2的平方根是±0.1 | ||||
D、
|
 已知在Rt△ABC中,a,b,c分别是角A,B,C的对边,∠C=90°,a=2,c=6,求sinA,cosA,tanA的值.
已知在Rt△ABC中,a,b,c分别是角A,B,C的对边,∠C=90°,a=2,c=6,求sinA,cosA,tanA的值. 如图,B,C,D是半径为6的⊙O上的三点,已知
如图,B,C,D是半径为6的⊙O上的三点,已知
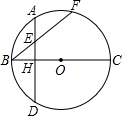 如图,已知BC是⊙O的直径,弦AD⊥BC于点H,与弦BF交于点E,AD=8,BH=2.
如图,已知BC是⊙O的直径,弦AD⊥BC于点H,与弦BF交于点E,AD=8,BH=2.