题目内容
 已知在Rt△ABC中,a,b,c分别是角A,B,C的对边,∠C=90°,a=2,c=6,求sinA,cosA,tanA的值.
已知在Rt△ABC中,a,b,c分别是角A,B,C的对边,∠C=90°,a=2,c=6,求sinA,cosA,tanA的值.考点:解直角三角形
专题:
分析:首先用勾股定理求出直角三角形中第三边的数值,进一步利用锐角三角函数的定义代入解决问题.
解答:解:∵∠C=90°,a=2,c=6,
∴b=
=
=4
,
∴sinA=
=
=
,
cosA=
=
=
,
tanA=
=
=
.
∴b=
| c2-a2 |
| 62-22 |
| 2 |
∴sinA=
| a |
| c |
| 2 |
| 6 |
| 1 |
| 3 |
cosA=
| b |
| c |
4
| ||
| 6 |
2
| ||
| 3 |
tanA=
| a |
| b |
| 2 | ||
4
|
| ||
| 4 |
点评:此题考查了解直角三角形,用到的知识点是锐角三角函数的定义,求锐角的三角函数值的方法:利用勾股定理求得三边,根据锐角三角函数的定义求出对应三角函数值即可.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
 有理数a,b在数轴上对应的点位置如下图所示,则下列试子中正确的是( )
有理数a,b在数轴上对应的点位置如下图所示,则下列试子中正确的是( )| A、a+b<0 |
| B、a+b>0 |
| C、a-b=0 |
| D、a-b<0 |
以下是代数式的是( )
| A、m=ab |
| B、(a+b)(a-b)=a2 |
| C、a+1-b2 |
| D、S=πR2 |
下列一组数:-2,-
,2,0,其中最小的是( )
| 1 |
| 2 |
| A、-2 | ||
B、-
| ||
| C、2 | ||
| D、0 |
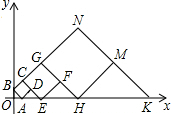 如图,在平面直角坐标系中,点A和点B分别在x轴和y轴的正半轴上,OA=OB=a,以线段AB为边在第一象限作正方形ABCD,CD的延长线交x轴于点E,再以CE为边作第二个正方形ECGF,…,依此方法作下去,则第2014个正方形的边长是
如图,在平面直角坐标系中,点A和点B分别在x轴和y轴的正半轴上,OA=OB=a,以线段AB为边在第一象限作正方形ABCD,CD的延长线交x轴于点E,再以CE为边作第二个正方形ECGF,…,依此方法作下去,则第2014个正方形的边长是 如图所示,在Rt△ABC中,∠BAC=90°,AB=AC,E、D分别是BC、AC上的点,且∠AED=45°,求证:△ABE∽△ECD.
如图所示,在Rt△ABC中,∠BAC=90°,AB=AC,E、D分别是BC、AC上的点,且∠AED=45°,求证:△ABE∽△ECD.