题目内容
 如图,在等边△ABC中,BC=8,D为AB中点,点E在BC上,点F在AC上,满足AF=3CF,DE平分∠BDF,则BE=
如图,在等边△ABC中,BC=8,D为AB中点,点E在BC上,点F在AC上,满足AF=3CF,DE平分∠BDF,则BE=考点:等边三角形的性质
专题:
分析:过D作DG⊥AC,EM⊥BD,EN⊥DF,FH⊥BC,根据等边三角形和直角三角形的性质,通过解直角三角形求得DG=2
,AF=6,CF=2,DF=2
,设BE=x,进一步求得EM=EN=
x,FH=
,CE=8-x,根据S△ABC=S△ADF+S△BED+S△DEF+S△EFC得出关于x的方程,解方程即可求得BE的长.
| 3 |
| 7 |
| ||
| 2 |
| 3 |
解答: 解:如图,过D作DG⊥AC,EM⊥BD,EN⊥DF,FH⊥BC,
解:如图,过D作DG⊥AC,EM⊥BD,EN⊥DF,FH⊥BC,
∵AB=BC=CA,BD=AD,AF=3CF,AB=8,
∴DG=2
,AF=6,CF=2,
∴DF=2
,
∵∠BDE=∠PDE,EM⊥BD,EN⊥DF,
∴EM=EN,
设BE=x,
∵∠B=∠C=60°,
∴EM=EN=
x,FH=
,CE=8-x,
∴S△ABC=S△ADF+S△BED+S△DEF+S△EFC=
×6×2
+
×4×
+
×2
×
+
(8-x)•
=
×8×8×
,
∴x=2
-2,
即BE=2
-2.
故答案为2
-2.
 解:如图,过D作DG⊥AC,EM⊥BD,EN⊥DF,FH⊥BC,
解:如图,过D作DG⊥AC,EM⊥BD,EN⊥DF,FH⊥BC,∵AB=BC=CA,BD=AD,AF=3CF,AB=8,
∴DG=2
| 3 |
∴DF=2
| 7 |
∵∠BDE=∠PDE,EM⊥BD,EN⊥DF,
∴EM=EN,
设BE=x,
∵∠B=∠C=60°,
∴EM=EN=
| ||
| 2 |
| 3 |
∴S△ABC=S△ADF+S△BED+S△DEF+S△EFC=
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 7 |
| ||
| 2 |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
∴x=2
| 7 |
即BE=2
| 7 |
故答案为2
| 7 |
点评:本题考查了等边三角形的性质,直角三角形的性质,以及解直角三角形,三角形的面积公式的应用等,作出辅助线构建直角三角形是关键.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
据江苏省统计局发布的《2013年江苏省国民经济和社会发展统计公报》显示,2013年我省国内生产总值约为57960亿元,这个国内生产总值用科学记数法可表示为( )
| A、5.796×104元 |
| B、5.796×1012元 |
| C、5.796×1011元 |
| D、5.796×1013元 |
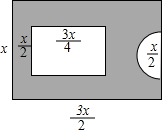 某中学一寝室前有一块长为
某中学一寝室前有一块长为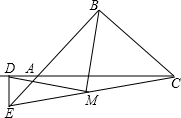 已知在Rt△ABC中,AB=BC.在Rt△ADE中,AD=DE;连接EC,取EC中点M,连接DM和BM.点D在CA的延长线上,点E在BA的延长线上,求证:BM=DM,BM⊥DM.
已知在Rt△ABC中,AB=BC.在Rt△ADE中,AD=DE;连接EC,取EC中点M,连接DM和BM.点D在CA的延长线上,点E在BA的延长线上,求证:BM=DM,BM⊥DM.