题目内容
20.“全民阅读”深入人心,读好书让人终身受益.为打造书香校园,满足同学们的读书需求,学校图书馆准备到新华书店采购文学名著和科技阅读两类图书.经了解,20本文学名著和40本科技阅读共需1520元,一本文学名著比一本科技阅读多22元(注:所采购的文学名著书价格都一样,所采购的科技阅读书价格都一样).(1)求每本文学名著和科技阅读各多少元?
(2)若学校要求购买科技阅读比文学名著多20本,科技阅读和文学名著总数不低于72本,总费用不超过2000元,请你为学校求出符合条件的购书方案.
(3)请在(2)的条件下,请你求出此次活动学校最多需投入资金多少元?
分析 (1)设每本文学名著x元,每本科技阅读y元,根据“20本文学名著和40本科技阅读共需1520元,一本文学名著比一本科技阅读多22元”,即可得出关于x、y的二元一次方程组,解之即可得出结论;
(2)设购买文学名著m本,则购买科技阅读(m+20)本,根据“科技阅读和文学名著总数不低于72本,总费用不超过2000元”,即可得出关于m的一元一次不等式组,解之即可得出m的取值范围,进而即可得出各种购书方案;
(3)设总共投入资金w元,根据总价=单价×数量即可得出w关于m的函数关系式,再根据一次函数的性质结合m的取值范围即可解决最值问题.
解答 解:(1)设每本文学名著x元,每本科技阅读y元,
根据题意得:$\left\{\begin{array}{l}{20x+40y=1520}\\{x=y+22}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=40}\\{y=18}\end{array}\right.$.
答:每本文学名著40元,每本科技阅读18元.
(2)设购买文学名著m本,则购买科技阅读(m+20)本,
根据题意得:$\left\{\begin{array}{l}{m+m+20≥72}\\{40m+18(m+20)≤2000}\end{array}\right.$,
解得:26≤m≤$\frac{820}{29}$,
∵m为正整数,
∴m=26、27、28,
∴m+20=46、47、48.
∴购买方案有:方案一:购买文学名著26本、科技阅读46本;方案二:购买文学名著27本、科技阅读47本;方案三:购买文学名著28本、科技阅读48本.
(3)设总共投入资金w元,
根据题意得:w=40m+18(m+20)=58m+360,
∵58>0,
∴当m=28时,w取最大值,最大值为1984.
∴此次活动学校最多需投入资金1984元.
点评 本题考查了一元一次不等式组的应用、二元一次方程组的应用以及一次函数的性质,解题的关键是:(1)找准等量关系列出关于x、y的二元一次方程组;(2)通过解一元一次不等式组找出各购买方案;(3)根据一次函数的性质解决最值问题.

 阅读快车系列答案
阅读快车系列答案| A. |  | B. |  | C. |  | D. |  |
| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
| A. | 个体 | B. | 总体 | C. | 总体的一个样本 | D. | 样本容量 |
| A. | 4 | B. | 5 | C. | 8 | D. | 10 |
| A. | 0.10×106 | B. | 1.0×105 | C. | 0.11×106 | D. | 1.1×105 |
| A. | $\sqrt{2}$a | B. | $\sqrt{3{a}^{2}}$ | C. | $\sqrt{{a}^{3}}$ | D. | $\sqrt{{a}^{4}}$ |
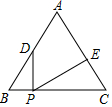 如图,在等边三角形ABC中,BC=8,点D是边AB上一点,且BD=3,点P是边BC上一动点,作∠DPE=60°,PE交边AC于点E,当CE=$\frac{16}{3}$时,满足条件的点P有且只有一个.
如图,在等边三角形ABC中,BC=8,点D是边AB上一点,且BD=3,点P是边BC上一动点,作∠DPE=60°,PE交边AC于点E,当CE=$\frac{16}{3}$时,满足条件的点P有且只有一个. 如图,CD是⊙O的直径,CD=4,∠ACD=20°,点B为弧AD 的中点,点P是直径CD 上的一个动点,则PA+PB的最小值为2.
如图,CD是⊙O的直径,CD=4,∠ACD=20°,点B为弧AD 的中点,点P是直径CD 上的一个动点,则PA+PB的最小值为2.