题目内容
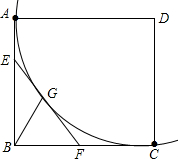 如图,正方形ABCD的边长为6,以D为圆心、DA为半径作⊙D,E在AB上,AE=2,EF切⊙D于G,交BC于F,
如图,正方形ABCD的边长为6,以D为圆心、DA为半径作⊙D,E在AB上,AE=2,EF切⊙D于G,交BC于F,(1)求证:BF=CF;
(2)求tan∠CBG的值.
考点:切线的性质,正方形的性质
专题:
分析:(1)利用切线长定理得出AE=EG=2,FC=FG,进而利用勾股定理得出FC的长,即可得出答案;
(2)利用(1)中所求,再得出△FGH∽△FEB,进而利用相似三角形的性质得出BH,HF的长,再利用锐角三角函数关系得出答案.
(2)利用(1)中所求,再得出△FGH∽△FEB,进而利用相似三角形的性质得出BH,HF的长,再利用锐角三角函数关系得出答案.
解答:(1)证明:∵EF切⊙D于G,以D为圆心、DA为半径作⊙D,
∴AE=EG=2,FC=FG,
不妨设FC=FG=x,
在△BEF中,
(2+x)2=42+(6-x)2
解得:x=3,
即FC=3,
故BF=6-3=3
即BF=FC;
(2)解:过G作GH⊥BF于H,
由(1)得:
∵BE=6-2=4,BF=3,
∴EF=5,
∵∠FBE=∠GHF,∠HFG=∠BFE,
∴△FGH∽△FEB,
∴
=
=
,
∴GH=
=
,HF=
∴BH=
,
∴tan∠CBG=
=
=2.
∴AE=EG=2,FC=FG,
不妨设FC=FG=x,
在△BEF中,
(2+x)2=42+(6-x)2
解得:x=3,
即FC=3,
故BF=6-3=3
即BF=FC;

(2)解:过G作GH⊥BF于H,
由(1)得:
∵BE=6-2=4,BF=3,
∴EF=5,
∵∠FBE=∠GHF,∠HFG=∠BFE,
∴△FGH∽△FEB,
∴
| GH |
| BE |
| FG |
| EF |
| HF |
| BF |
∴GH=
| 4×3 |
| 5 |
| 12 |
| 5 |
| 9 |
| 5 |
∴BH=
| 6 |
| 5 |
∴tan∠CBG=
| GH |
| BH |
| ||
|
点评:此题主要考查了切线的性质以及相似三角形的判定与性质以及勾股定理等知识,得出△FGH∽△FEB求出BH,HF的长是解题关键.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
 如图,在梯形ABCD中,AD∥BC,E、F分别是腰AB、DC的中点,四边形AEFD与四边形EBCF相似吗?为什么?
如图,在梯形ABCD中,AD∥BC,E、F分别是腰AB、DC的中点,四边形AEFD与四边形EBCF相似吗?为什么? 如图,有一块长为6.5单位长度,宽为2单位长度的长方形纸片,请把它分成6块,再拼成一个正方形,先在图中画出分割线,再画出拼后的图形,并标出相应的数据.
如图,有一块长为6.5单位长度,宽为2单位长度的长方形纸片,请把它分成6块,再拼成一个正方形,先在图中画出分割线,再画出拼后的图形,并标出相应的数据.
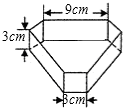 如图所示,是一种“口子窖”酒的包装纸盒,它的侧面由长方形和正方形组成.经测量,底面六变形有三条边的长是9cm,有三条边的长是3cm,每个内角都是120°,该六棱柱的高是3cm,请你设计一种裁剪方案,使之能制作这种无盖的包装盒.
如图所示,是一种“口子窖”酒的包装纸盒,它的侧面由长方形和正方形组成.经测量,底面六变形有三条边的长是9cm,有三条边的长是3cm,每个内角都是120°,该六棱柱的高是3cm,请你设计一种裁剪方案,使之能制作这种无盖的包装盒.