题目内容
直角三角形的斜边长是|x-3|,一条直角边的长是|4-3x|,那么当另一条直角边达到最大时,这个直角三角形的周长的范围大致在( )
| A、3与4之间 |
| B、4与5之间 |
| C、5与6之间 |
| D、6与7之间 |
考点:勾股定理
专题:
分析:根据勾股定理首先表示出另一条直角边,由此求出其最大值,进而求出斜边和直角边的最大值,则这个直角三角形的周长的范围大致可求.
解答:解:由勾股定理得:另一条直角边为:
=
∴这条边最大时,x=
;最大值=
;
此时斜边=|
-3|=
;
直角边=|4-
|=
;
∴周长=
+
+
≈4.2675;
∴范围是4与5之间,
故选B.
| (x-3)2-(4-3x)2 |
-8(x-
|
∴这条边最大时,x=
| 9 |
| 8 |
5
| ||
| 4 |
此时斜边=|
| 9 |
| 8 |
| 15 |
| 8 |
直角边=|4-
| 27 |
| 8 |
| 5 |
| 8 |
∴周长=
| 15 |
| 8 |
| 5 |
| 8 |
5
| ||
| 4 |
∴范围是4与5之间,
故选B.
点评:本题考查了勾股定理的运用以及最大值的问题,此题对学生的计算能力要求很高,题目的难度不小.

练习册系列答案
相关题目
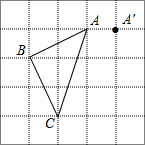 如图,在边长均为1cm的正方形网格中,△ABC的三个顶点和点A′均在格点上.将△ABC向右平移,使点A平移至点A′处,得到△A′B′C′.在图中画出△A′B′C′,并求边AC扫过的图形面积.
如图,在边长均为1cm的正方形网格中,△ABC的三个顶点和点A′均在格点上.将△ABC向右平移,使点A平移至点A′处,得到△A′B′C′.在图中画出△A′B′C′,并求边AC扫过的图形面积. 如图,已知菱形ABCD的对角线相交于点O,延长AB至点E,使BE=AB,连接CE,若∠E=70°,则∠BAO的度数为
如图,已知菱形ABCD的对角线相交于点O,延长AB至点E,使BE=AB,连接CE,若∠E=70°,则∠BAO的度数为 已知;如图,AD=BC,AC=BD,求证:AE=EB.
已知;如图,AD=BC,AC=BD,求证:AE=EB. 小明和小亮一天在广场上玩,看见有人在设摊“摸彩”.
小明和小亮一天在广场上玩,看见有人在设摊“摸彩”.