题目内容
4.如图1,正方形ABCD的边长为12cm,点P在正方形的边上从A→B→C以4cm/s的速度运动,同时点Q在正方形的边上从C→D以1cm/s的速度运动,设运动时间为t秒(0<t≤6).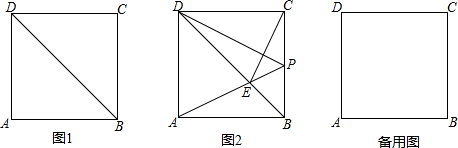
(1)当PQ∥BD时,求t的值;
(2)如图2,当点P在BC边上时,连接PA交BD于点E,连接CE,若DP⊥CE,求t的值;
(3)当点A到PQ所在直线的距离为12cm时,求出t的值.
分析 (1)当PQ∥BD时,则BP=DQ,根据题意得出方程,解方程即可;
(2)延长CE交AB于F,由正方形的性质得出∠BAD=∠BCD=∠ABC=90°,AB=BC=CD,∠ABE=∠CBE=45°,由AAS证明△CDP≌△BCF,得出CP=BF,由SAS证明△ABE≌△CBE,得出∠4=∠2,再由ASA证明△ABP≌△CBF,得出BP=BF,得出方程,解方程即可;
(3)当点A到PQ所在直线的距离为12cm时,则PQ在CD上,即P点与C点重合,即可求出t的值.
解答 解:(1)当PQ∥BD时,如图1所示: 则BP=DQ,
则BP=DQ,
根据题意得:CQ=t,DQ=12-t,BP=4t-12,
∴4t-12=12-t,
解得:t=$\frac{24}{5}$;
(2)延长CE交AB于F,如图2所示:
∵四边形ABCD是正方形,
∴∠BAD=∠BCD=∠ABC=90°,AB=BC=CD,∠ABE=∠CBE=45°,
∴∠1+∠2=90°,
∵DP⊥CE,
∴∠CGD=90°,
∴∠1+∠3=90°,
∴∠3=∠2,
在△CDP和△BCF中,
$\left\{\begin{array}{l}{∠PCD=∠FBC}&{\;}\\{∠3=∠2}&{\;}\\{CD=BC}&{\;}\end{array}\right.$,
∴△CDP≌△BCF(AAS),
∴CP=BF,
∵BP=4t-12,
∴BF=CP=12-(4t-12)=24-4t,
在△ABE和△CBE中,
$\left\{\begin{array}{l}{AB=CB}&{\;}\\{∠ABE=∠CBE}&{\;}\\{BE=BE}&{\;}\end{array}\right.$,
∴△ABE≌△CBE(SAS),
∴∠4=∠2,
在△ABP和△CBF中,
$\left\{\begin{array}{l}{∠4=∠2}&{\;}\\{AB=CB}&{\;}\\{∠ABP=∠CBF}&{\;}\end{array}\right.$,
∴△ABP≌△CBF(ASA),
∴BP=BF,
即4t-12=24-4t,
解得:t=$\frac{9}{2}$;
即若DP⊥CE,t的值为$\frac{9}{2}$;
(3)当点A到PQ所在直线的距离为12cm时,如图3所示:
则PQ在CD上,
即P点与C点重合,
t=(AB+BC)÷4=24÷4=6(s).
点评 本题是四边形综合题目,考查了正方形的性质、全等三角形的判定与性质、解方程等知识;本题综合性强,难度较大,特别是(2)中,需要三次证明三角形全等才能得出结果.

| A. | x轴上 | B. | y轴上 | C. | 原点 | D. | 坐标轴上 |

| A. | 随n的变化而变化 | B. | 不变,总是0 | C. | 不变,定值为1 | D. | 不变,定值为2 |
| A. | y3<y2<y1 | B. | y2>y1>y3 | C. | y1<y2<y3 | D. | y2<y1<y3 |
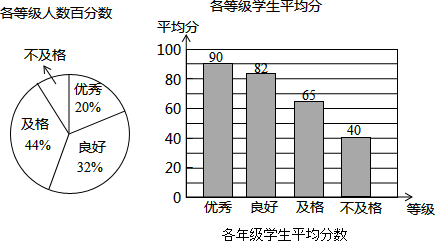
 (1)计算:$\root{3}{-8}$-|-$\sqrt{3}$|-$\sqrt{3}$($\sqrt{3}$-1)
(1)计算:$\root{3}{-8}$-|-$\sqrt{3}$|-$\sqrt{3}$($\sqrt{3}$-1)