题目内容
14．已知关于x的不等式组$\left\{\begin{array}{l}{x-a≥0}\\{3-2x＞-1}\end{array}\right.$的整数解共有7个，则a的取值范围为-6＜a≤-5．分析 先求出不等式组的解集，根据已知和不等式组的解集得出关于a的不等式组即可．
解答 解：$\left\{\begin{array}{l}{x-a≥0①}\\{3-2x＞-1②}\end{array}\right.$
∵解不等式①得：x≥a，
解不等式②得：x＜2，
∴不等式组的解集是a≤x＜2，
∵关于x的不等式组$\left\{\begin{array}{l}{x-a≥0}\\{3-2x＞-1}\end{array}\right.$的整数解共有7个，
∴-6＜a≤-5，
故答案为：-6＜a≤-5．
点评 本题考查了解一元一次不等式组，不等式组的整数解的应用，解此题的关键是能根据已知不等式组的整数解和不等式的解集得出关于a的不等式组，难度适中．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
9．若a=97，b=275，c=814，则a、b、c的大小关系是（ ）
| A． | a＞b＞c | B． | b＞c＞a | C． | a＞c＞b | D． | c＞b＞a |
19．下列不等式组是一元一次不等式组的是（ ）
| A． | $\left\{\begin{array}{l}{x-y＞0}\\{x+y＜0}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{x+\frac{1}{3}＞\frac{1}{2}x}\\{3x≠4x-1}\end{array}\right.$ | ||
| C． | $\left\{\begin{array}{l}{{x}^{2}+x-2＞0}\\{3x＜0}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{3x+2y=0}\\{x＞-y}\end{array}\right.$ |
13．
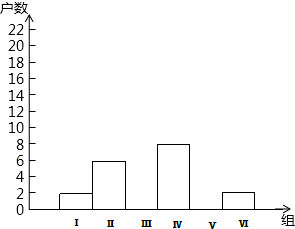今年是我国施行“清明”小长假的第二年，在长假期间，某校团委要求学生参加一项社会调查活动．九年级学生小青想了解她所居住的小区500户居民的家庭人均收入情况，从中随机调查了40户居民家庭的人均收入情况（收入取整数，单位：元）并绘制了如下的分布表和分布图：
根据以上提供的信息，解答下列问题：
（1）补全分布表、分布图；
（2）这40户家庭收入的中位数落在哪一个小组？
（3）被调查的家庭中，参加“清明扫墓“活动的家庭统计如表：
问：估计该小区共有多少户家庭参加了扫墓活动．
今年是我国施行“清明”小长假的第二年，在长假期间，某校团委要求学生参加一项社会调查活动．九年级学生小青想了解她所居住的小区500户居民的家庭人均收入情况，从中随机调查了40户居民家庭的人均收入情况（收入取整数，单位：元）并绘制了如下的分布表和分布图：| 分组 | 户数 | 百分比 |
| Ⅰ：600-799 | 2 | 0.05 |
| Ⅱ：800-999 | 6 | 0.15 |
| Ⅲ：1000-1199 | 0.45 | |
| Ⅳ：1200-1399 | 8 | 0.20 |
| Ⅴ：1400-1599 | ||
| Ⅵ：1600-1800 | 2 | 0.05 |
| 合计 | 40 | 1.00 |
（1）补全分布表、分布图；
（2）这40户家庭收入的中位数落在哪一个小组？
（3）被调查的家庭中，参加“清明扫墓“活动的家庭统计如表：
| 收入情况 | 600-799 | 800-999 | 1000-1199 | 1200-1399 | 1400-1599 | 1600-1800 |
| $\frac{参加扫墓家庭数}{被调查家庭数}$ | $\frac{1}{2}$ | $\frac{1}{3}$ | $\frac{1}{6}$ | $\frac{1}{4}$ | 1 | 1 |