题目内容
1.有一列数:-1,$\frac{3}{4}$,-$\frac{5}{9}$,$\frac{7}{16}$,-$\frac{9}{25}$,$\frac{11}{36}$…按此规律排列,则第9个数是-$\frac{17}{81}$.分析 根据数列得出第n个数为(-1)n•$\frac{2n-1}{{2}^{n}}$,据此可得.
解答 解:∵第1个数-1=(-1)1×$\frac{2×1-1}{{1}^{2}}$,
第2个数$\frac{3}{4}$=(-1)2×$\frac{2×2-1}{{2}^{2}}$,
第3个数-$\frac{5}{9}$=(-1)3×$\frac{2×3-1}{{3}^{2}}$,
…
∴第9个数为(-1)9×$\frac{2×9-1}{{9}^{2}}$=-$\frac{17}{81}$,
故答案为:-$\frac{17}{81}$.
点评 本题主要考查数字的变化规律,根据数列得出第n个数为(-1)n•$\frac{2n-1}{{2}^{n}}$是解题的关键.

练习册系列答案
相关题目
17.如图所示,数轴的单位长度为1,如果点M、N表示的数的绝对值相等,那么点M表示的数是( )


| A. | -4 | B. | -3 | C. | -2 | D. | 3 |
16.已知平面内有A,B,C,D四点,过其中的两点画一条直线,一共可以画( )直线.
| A. | 1条 | B. | 4条 | C. | 6条 | D. | 1条、4条或6条 |
13.在圆心角为120°的扇形AOB中,半径OA=6,则扇形AOB的面积是( )
| A. | 6π | B. | 8π | C. | 12π | D. | 24π |
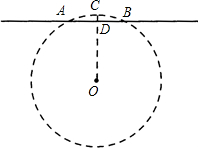 今有圆材,埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问径几何.(选自《九章算术》卷第九“句股”中的第九题,1尺=10寸).
今有圆材,埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问径几何.(选自《九章算术》卷第九“句股”中的第九题,1尺=10寸).