题目内容
11. 如图,某小区①号楼与⑪号楼隔河相望,李明家住在①号楼,他很想知道⑪号楼的高度,于是他做了一些测量,他先在B点测得C点的仰角为60°,然后到42米高的楼顶A处,测得C点的仰角为30°,请你帮助李明计算⑪号楼的高度CD.
如图,某小区①号楼与⑪号楼隔河相望,李明家住在①号楼,他很想知道⑪号楼的高度,于是他做了一些测量,他先在B点测得C点的仰角为60°,然后到42米高的楼顶A处,测得C点的仰角为30°,请你帮助李明计算⑪号楼的高度CD.
分析 作AE⊥CD,用BD可以分别表示DE,CD的长,根据CD-DE=AB,即可求得BC的长,即可解题.
解答  解:作AE⊥CD,
解:作AE⊥CD,
∵CD=BD•tan60°=$\sqrt{3}$BD,CE=BD•tan30°=$\frac{\sqrt{3}}{3}$BD,
∴AB=CD-CE=$\frac{2\sqrt{3}}{3}$BD,
∴BD=21$\sqrt{3}$m,
CD=BD•tan60°=$\sqrt{3}$BD=63m.
答:⑪建筑物的高度CD为63m.
点评 本题考查了直角三角形中三角函数的应用,考查了特殊角的三角函数值,本题中求的BD的长是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.《九章算术》中注有“今两算得失相反,要令正负以名之”,意思是:今有两数若其意义相反,则分别叫做正数与负数,若气温为零上10℃记作+10℃,则-3℃表示气温为( )
| A. | 零上3℃ | B. | 零下3℃ | C. | 零上7℃ | D. | 零下7℃ |
19.($\frac{1}{3}$)-2的相反数是( )
| A. | 9 | B. | -9 | C. | $\frac{1}{9}$ | D. | -$\frac{1}{9}$ |
16.下列运算正确的是( )
| A. | |$\sqrt{2}-1$|=$\sqrt{2}-1$ | B. | x3•x2=x6 | C. | x2+x2=x4 | D. | (3x2)2=6x4 |
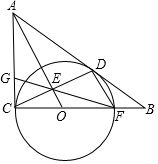 如图,⊙O与Rt△ABC的直角边AC和斜边AB分别相切于点C、D,与边BC相交于点F,OA与CD相交于点E,连接FE并延长交AC边于点G.
如图,⊙O与Rt△ABC的直角边AC和斜边AB分别相切于点C、D,与边BC相交于点F,OA与CD相交于点E,连接FE并延长交AC边于点G. 如图,在平面直角坐标系中,Rt△AOB的斜边OA在x轴的正半轴上,∠OBA=90°,且tan∠AOB=$\frac{1}{2}$,OB=2$\sqrt{5}$,反比例函数y=$\frac{k}{x}$的图象经过点B.
如图,在平面直角坐标系中,Rt△AOB的斜边OA在x轴的正半轴上,∠OBA=90°,且tan∠AOB=$\frac{1}{2}$,OB=2$\sqrt{5}$,反比例函数y=$\frac{k}{x}$的图象经过点B.