题目内容
1.在圆中,30°的圆周角所对的弦的长度为$\sqrt{3}$,则这个圆的半径是$\sqrt{3}$.分析 先求出弦所对的圆心角为60°,则可判断这条弦与两半径所组成的三角形是等边三角形,从而得出圆的半径.
解答 解:∵∠BAC=30°,
∴∠BOC=60°,
∴△BOC是等边三角形,
∴OB=OC=BC=$\sqrt{3}$,即这个圆的半径为$\sqrt{3}$.
故答案为:$\sqrt{3}$.
点评 本题考查了圆周角定理,解答本题的关键是熟练掌握在同圆或等圆中,同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半.

练习册系列答案
相关题目
11.据统计,长春市主城区2015年上半年机动车数量突破1000000辆大关,1000000这个数用科学记数法表示为( )
| A. | 1×107 | B. | 0.1×107 | C. | 1×106 | D. | 10×101 |
6. 如图,所示的几何体的正视图是( )
如图,所示的几何体的正视图是( )
 如图,所示的几何体的正视图是( )
如图,所示的几何体的正视图是( )| A. |  | B. |  | C. |  | D. |  |
13.要使函数y=$\sqrt{x-1}$有意义,自变量x的取值范围是( )
| A. | x≥1 | B. | x≤1 | C. | x>1 | D. | x<1 |
10.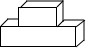 如图,观察这个立体图形,它的俯视图是( )
如图,观察这个立体图形,它的俯视图是( )
 如图,观察这个立体图形,它的俯视图是( )
如图,观察这个立体图形,它的俯视图是( )| A. |  | B. |  | C. |  | D. |  |