题目内容
1.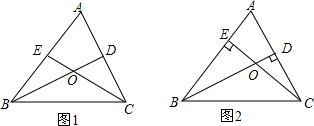 如图,
如图,(1)BD、CE是△ABC的角平分线,
①若∠A=50°,求∠BOC的度数;
②若∠A=α,则∠BOC=90°+$\frac{1}{2}$α
(2)BD、CE是△ABC的高,
①若∠A=50°,求∠BOC的度数;
②若∠A=α,则∠BOC=180°-α.
分析 (1)由于∠A=50°,根据三角形的内角和定理,得∠ABC与∠ACB的度数和,再由角平分线的定义,得∠OBC+∠OCB的度数,进而求出∠BOC的度数;
(2)因为BD、CE均为△ABC的高,则有AEC=∠ADB=∠BDC=90°;又知∠A=50°,可根据三角形的内角和定理得到∠ACE=90°-∠A=90°-50°=40°,最后依据三角形的外角性质定理即三角形的一个外角等于与它不相邻的两个内角之和,得到∠BOC=∠BDC+∠ACE=90°+40°=130°.
解答 解:(1)①∵∠A=50°,
∴∠ABC+∠ACB=180°-50°=130°,
∵BE、CF是△ABC的角平分线,
∴∠OBC+∠OCB=$\frac{1}{2}$(∠ABC+∠ACB)=65°,
∴∠BOC=180°-(∠OBC+∠OCB)=180°-65°=115°;
②∠BOC=180°-$\frac{1}{2}$(180°-∠A)=90°+$\frac{1}{2}$α,
故答案为:90°+$\frac{1}{2}$α;:
(2)①∵BD、CE均为△ABC的高,
∴∠AEC=∠ADB=∠BDC=90°,
∵∠A=50°,
∴∠ACE=90°-∠A=90°-50°=40°.
则∠BOC=∠BDC+∠ACE=90°+40°=130°;
②∠BOC=90°+(90°-α)=180°-α,
故答案为:180°-α
点评 本题主要考查三角形的外角性质及三角形的内角和定理.解题的关键是熟练掌握三角形的外角性质定理,即三角形的一个外角等于与它不相邻的两个内角之和.

练习册系列答案
相关题目
11.下列图形中,是中心对称图形但不是轴对称图形的是( )
| A. | 平行四边形 | B. | 矩形 | C. | 菱形 | D. | 等腰梯形 |
10.下列各式中结果为2x4的是( )
| A. | x4•x4 | B. | x4+x4 | C. | 2x2+x2 | D. | 2x•x4 |

 如图,AB=5,AC=3,AD是△ABC的中线,则△ABD与△ADC的周长相差多少?
如图,AB=5,AC=3,AD是△ABC的中线,则△ABD与△ADC的周长相差多少? 如图所示,在一次暴风雨后,一棵大树从离地面3m处被折断,经测量树的顶端与地面的接触点离树根部的距离为2m,若在该树正上方离地面7m处有高压电线l,请判断,该树在折断前是否接触到电线?并说明你的理由.
如图所示,在一次暴风雨后,一棵大树从离地面3m处被折断,经测量树的顶端与地面的接触点离树根部的距离为2m,若在该树正上方离地面7m处有高压电线l,请判断,该树在折断前是否接触到电线?并说明你的理由.