题目内容
5.某公园正在举行郁金香花展,现从红、黄两种郁金香中,各抽出6株,测得它们离地面的高度分别如下(单位cm):红:54、44、37、36、35、34; 黄:48、35、38、36、43、40;
已知它们的平均高度均是40cm,请判断哪种颜色的郁金香样本长得整齐?黄.(填“红”或“黄”)
分析 先根据方差公式S2=$\frac{1}{n}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+…+(xn-$\overline{x}$)2]分别求出红颜色和黄颜色的方差,然后进行比较,即可得出答案.
解答 解:红颜色的郁金香的方差是:$\frac{1}{6}$[(54-40)2+(44-40)2+(37-40)2+(36-40)2+(35-40)2+(34-40)2]≈49.67,
黄颜色的郁金香的方差是:$\frac{1}{6}$[(48-40)2+(35-40)2+(38-40)2+(36-40)2+(43-40)2+(40-40)2]≈29.67,
∵S2红>S2黄,
∴黄颜色的郁金香样本长得整齐;
故答案为:黄.
点评 本题考查方差的定义与意义:一般地设n个数据,x1,x2,…xn的平均数为$\overline{x}$,则方差S2=$\frac{1}{n}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+…+(xn-$\overline{x}$)2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.

练习册系列答案
相关题目
17.某学习小组有6人,在一次数学测验中的成绩分别是:115,100,105,90,105,85,则他们成绩的极差和众数分别是( )
| A. | 30和115 | B. | 30和105 | C. | 20和100 | D. | 15和105 |
14.要说明“若两个单项式的次数相同,则它们是同类项”是假命题,可以举的反例是( )
| A. | 2ab和3ab | B. | 2a2b和3ab2 | C. | 2ab和2a2b2 | D. | 2a3和-2a3 |
15.下列因式分解正确的是( )
| A. | x2-2x-1=(x-1)2 | B. | 2x2-2=2(x+1)(x-1) | C. | x2y-xy=y(x2-x) | D. | x2-2x+2=(x-1)2+1 |
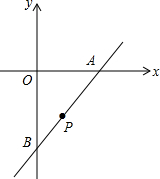 已知直线y=x-4与x轴、y轴分别交于A、B两点,点P(1,m)在直线AB上.
已知直线y=x-4与x轴、y轴分别交于A、B两点,点P(1,m)在直线AB上.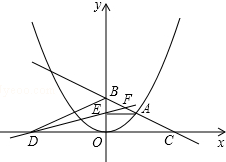 如图,在平面直角坐标系中,A是抛物线y=x2上的一个动点,且点A在第一象限内.AE⊥y轴于点E,点B坐标为(0,6),直线AB交x轴于点C,点D与点C关于y轴对称,直线DE与AB相交于点F,连结BD.设线段AE的长为a,△BED的面积为S.
如图,在平面直角坐标系中,A是抛物线y=x2上的一个动点,且点A在第一象限内.AE⊥y轴于点E,点B坐标为(0,6),直线AB交x轴于点C,点D与点C关于y轴对称,直线DE与AB相交于点F,连结BD.设线段AE的长为a,△BED的面积为S. 如图,在一张长为5,宽为4的矩形纸片上,现要剪下一个腰长为3的等腰三角形(要求:等腰三角形的一个顶点与矩形的一个顶点重合,其余的两个顶点在矩形的边上),则剪下的等腰三角形的面积为$\frac{9}{2}$或2$\sqrt{2}$或$\frac{3}{2}$$\sqrt{5}$.
如图,在一张长为5,宽为4的矩形纸片上,现要剪下一个腰长为3的等腰三角形(要求:等腰三角形的一个顶点与矩形的一个顶点重合,其余的两个顶点在矩形的边上),则剪下的等腰三角形的面积为$\frac{9}{2}$或2$\sqrt{2}$或$\frac{3}{2}$$\sqrt{5}$.