题目内容
16.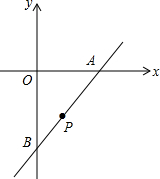 已知直线y=x-4与x轴、y轴分别交于A、B两点,点P(1,m)在直线AB上.
已知直线y=x-4与x轴、y轴分别交于A、B两点,点P(1,m)在直线AB上.(1)在y轴上找一点M,使MP+MA最小;
(2)在x轴上找一点N,使PN最小.
分析 (1)作A点关于y轴的对称点A′,连接PA′交y轴于M,此时MP+MA=MP+MA′=PA′,根据两点之间线段最短可知此时MP+MA最小,求得A′、P的坐标,利用待定系数法即可求得直线PA′的解析式,进而求得M的坐标;
(2)作PN⊥x轴于N,根据垂线段最短可知PN最小;根据P的坐标即可求得N的坐标.
解答  解:(1)如图,作A点关于y轴的对称点A′,连接PA′交y轴于M,此时MP+MA=MP+MA′=PA′,根据两点之间线段最短可知此时MP+MA最小,
解:(1)如图,作A点关于y轴的对称点A′,连接PA′交y轴于M,此时MP+MA=MP+MA′=PA′,根据两点之间线段最短可知此时MP+MA最小,
∵点P(1,m)在直线AB上,
∴m=1-4=-3,
∴P(1,-3),
由直线y=x-4可知A(4,0),
∴A′(-4,0),
设直线PA′的解析式为y=kx+b,
∴$\left\{\begin{array}{l}{k+b=-3}\\{-4k+b=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-\frac{3}{5}}\\{b=-\frac{12}{5}}\end{array}\right.$,
∴M(0,-$\frac{12}{5}$).
(2)如图,作PN⊥x轴于N,根据垂线段最短可知PN最小;
∵P(1,-3),
∴N(1,0).
点评 本题考查了一次函数图象上点的坐标特征,轴对称-最短路线问题,两点之间线段最短以及垂线段最短是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
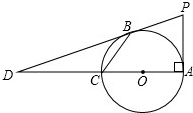 如图所示,AC为⊙O的直径且PA⊥AC,BC是⊙O的一条弦,直线PB交直线AC于点D,且PB=PA.
如图所示,AC为⊙O的直径且PA⊥AC,BC是⊙O的一条弦,直线PB交直线AC于点D,且PB=PA.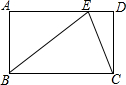 已知:如图,点E是矩形ABCD的边AD上一点,BE=AD,AE=8,现有甲乙两人同时从E点出发,分别沿EC,ED方向前进,甲的速度是乙的$\sqrt{10}$倍,甲到达目的地C点的同时乙恰好到达终点D处.
已知:如图,点E是矩形ABCD的边AD上一点,BE=AD,AE=8,现有甲乙两人同时从E点出发,分别沿EC,ED方向前进,甲的速度是乙的$\sqrt{10}$倍,甲到达目的地C点的同时乙恰好到达终点D处.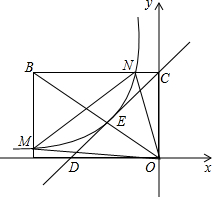 如图,矩形OABC的边OA在x轴的负半轴上,边OC在y轴的正半轴上,且OA=2OC,直线y=x+b过点C,并且交对角线OB于点E,交x轴于点D,反比例函数y=$\frac{a}{x}$过点E且交AB于点M,交BC于点N,连接MN、OM、ON,若△OMN的面积是$\frac{80}{9}$,则a+b=1.
如图,矩形OABC的边OA在x轴的负半轴上,边OC在y轴的正半轴上,且OA=2OC,直线y=x+b过点C,并且交对角线OB于点E,交x轴于点D,反比例函数y=$\frac{a}{x}$过点E且交AB于点M,交BC于点N,连接MN、OM、ON,若△OMN的面积是$\frac{80}{9}$,则a+b=1.