题目内容
6.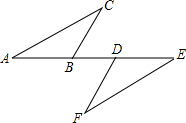 如图,点A、B、D、E在同一直线上,AD=EB,BC∥DF,∠C=∠F,求证:AC=EF.
如图,点A、B、D、E在同一直线上,AD=EB,BC∥DF,∠C=∠F,求证:AC=EF.
分析 根据BC∥DF证得∠CBD=∠FDB,利用等角的补角相等证得∠ABC=∠EDF,然后根据AD=EB得到AB=ED,利用AAS证明两三角形全等即可.
解答 证明:∵AD=EB
∴AD-BD=EB-BD,即AB=ED
又∵BC∥DF,
∴∠CBD=∠FDB
∴∠ABC=∠EDF
在△ABC和△EDF中,
$\left\{\begin{array}{l}{∠C=∠F}\\{∠ABC=∠EDF}\\{AB=ED}\end{array}\right.$
∴△ABC≌△EDF(AAS),
∴AC=EF
点评 本题考查了全等三角形的判定与性质,解题的关键是选择最合适的方法证明两三角形全等.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.将点A(1,-2)向右平移2个单位,再向上平移3个单位得B点,则B的坐标为( )
| A. | (-1,1) | B. | (-1,-5) | C. | (3,1) | D. | (3,-5) |
14.下列说法中错误的是( )
| A. | 对角线互相平分的四边形是平行四边形 | |
| B. | 对角线相等的四边形是矩形 | |
| C. | 对角线互相垂直平分的四边形是菱形 | |
| D. | 对角线互相垂直平分且相等的四边形是正方形 |
 已知:如图,在△ABC中,BD⊥AC于点D,E为BC上一点,过E点作EF⊥AC,垂足为F,过点D作DH∥BC交AB于点H.
已知:如图,在△ABC中,BD⊥AC于点D,E为BC上一点,过E点作EF⊥AC,垂足为F,过点D作DH∥BC交AB于点H.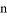 元,而甲型号手机仍按今年的售价销售,要使(2)中所有方案获利相同,
元,而甲型号手机仍按今年的售价销售,要使(2)中所有方案获利相同, =__________时,分式
=__________时,分式 的值为0;
的值为0;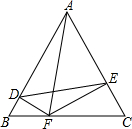 △ABC是边长为4个单位长度的等边三角形,点F是边BC上的点,FD⊥AB,FE⊥AC,
△ABC是边长为4个单位长度的等边三角形,点F是边BC上的点,FD⊥AB,FE⊥AC,