题目内容
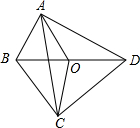 如图,在四边形ABCD中,∠BAD=∠BCD=90°,O为BD的中点.
如图,在四边形ABCD中,∠BAD=∠BCD=90°,O为BD的中点.(1)若AC=8,BD=10,求△A0C的周长.
(2)若∠ABD=60°,∠CBD=50°,求∠A0C和∠OCA的度数.
考点:直角三角形斜边上的中线
专题:
分析:(1)根据直角三角形斜边上中线性质求出AO和CO,即可得出答案;
(2)根据直角三角形斜边上中线性质求出AO=OB,求出∠OAB=∠ABD=60°,根据三角形内角和定理得出∠AOB=60°,同理∠COB=80°,求出∠AOC即可;根据OA=OC得出∠OCA=∠OAC=
(180°-∠AOC),代入求出即可.
(2)根据直角三角形斜边上中线性质求出AO=OB,求出∠OAB=∠ABD=60°,根据三角形内角和定理得出∠AOB=60°,同理∠COB=80°,求出∠AOC即可;根据OA=OC得出∠OCA=∠OAC=
| 1 |
| 2 |
解答:解:(1)∵∠BAD=∠BCD=90°,O为BD的中点,AC=8,BD=10,
∴AO=
BD=5,CO=
BD=5,
∴△A0C的周长为AC+OA+OC=10+5+5=20;
(2)∵∠BAD=90°,O为BD中点,
∴AO=OB,
∵∠ABD=60°,
∴∠OAB=∠ABD=60°,
∴∠AOB=180°-60°-60°=60°,
同理∠COB=180°-50°-50°=80°,
∴∠AOC=∠AOB+∠COB=60°+80°=140°;
∵OA=OC,
∴∠OCA=∠OAC=
(180°-∠AOC)=20°.
∴AO=
| 1 |
| 2 |
| 1 |
| 2 |
∴△A0C的周长为AC+OA+OC=10+5+5=20;
(2)∵∠BAD=90°,O为BD中点,
∴AO=OB,
∵∠ABD=60°,
∴∠OAB=∠ABD=60°,
∴∠AOB=180°-60°-60°=60°,
同理∠COB=180°-50°-50°=80°,
∴∠AOC=∠AOB+∠COB=60°+80°=140°;
∵OA=OC,
∴∠OCA=∠OAC=
| 1 |
| 2 |
点评:本题考查了直角三角形斜边上中线性质,等腰三角形性质,三角形的内角和定理的应用,注意:直角三角形斜边上的中线等于斜边的一半.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
一个三角形三边之比为4:6:7,与之相似的另一个三角形最长边为28cm,则最短边为( )
| A、12cm | B、16cm |
| C、24cm | D、49cm |