题目内容
3.已知$\sqrt{a-1}+(b+3)^{2}$=0,则M(a,b)关于x轴对称的点的坐标为(1,3).分析 首先利用偶次方以及二次根式的性质得出a,b的值,再利用关于x轴对称点的坐标特点:横坐标不变,纵坐标互为相反数.即点P(x,y)关于x轴的对称点P′的坐标是(x,-y),即可得出答案.
解答 解:∵$\sqrt{a-1}+(b+3)^{2}$=0,
∴a-1=0,b+3=0,
解得:a=1,b=-3,
则M(a,b)为:(1,-3),
故M(a,b)关于x轴对称的点的坐标为:(1,3).
故答案为:(1,3).
点评 此题主要考查了偶次方以及二次根式的性质和关于x轴对称点的性质,正确记忆关于坐标轴对称点的性质是解题关键.

练习册系列答案
相关题目
13.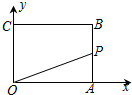 如图,已知矩形OABC,A(4,0),C(0,4),动点P从点A出发,沿A-B-C-O的路线匀速运动,设动点P的运动路程为t,△OAP的面积为S,则下列能大致反映S与t之间关系的图象是( )
如图,已知矩形OABC,A(4,0),C(0,4),动点P从点A出发,沿A-B-C-O的路线匀速运动,设动点P的运动路程为t,△OAP的面积为S,则下列能大致反映S与t之间关系的图象是( )
 如图,已知矩形OABC,A(4,0),C(0,4),动点P从点A出发,沿A-B-C-O的路线匀速运动,设动点P的运动路程为t,△OAP的面积为S,则下列能大致反映S与t之间关系的图象是( )
如图,已知矩形OABC,A(4,0),C(0,4),动点P从点A出发,沿A-B-C-O的路线匀速运动,设动点P的运动路程为t,△OAP的面积为S,则下列能大致反映S与t之间关系的图象是( )| A. |  | B. |  | C. | 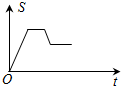 | D. | 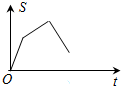 |
18.以面积为9cm2的正方形的对角线为边长的正方形面积为( )
| A. | 18cm2 | B. | 20cm2 | C. | 24cm2 | D. | 28cm2 |
13. 如图,在△ABC中,两条中线BE,CD相交于点O,则S△DOE:S△BCE=( )
如图,在△ABC中,两条中线BE,CD相交于点O,则S△DOE:S△BCE=( )
 如图,在△ABC中,两条中线BE,CD相交于点O,则S△DOE:S△BCE=( )
如图,在△ABC中,两条中线BE,CD相交于点O,则S△DOE:S△BCE=( )| A. | 1:3 | B. | 1:4 | C. | 1:6 | D. | 2:3 |
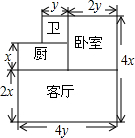 如图是一所住宅的建筑平面图(图中长度单位:m).
如图是一所住宅的建筑平面图(图中长度单位:m). 已知正比例函数y=$\frac{1}{2}$x的图象与一次函数y=kx-3的图象相交于点(2,a).
已知正比例函数y=$\frac{1}{2}$x的图象与一次函数y=kx-3的图象相交于点(2,a).