题目内容
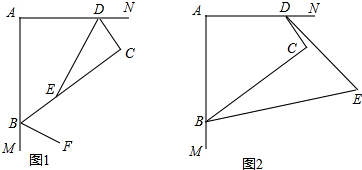
 如图是一张矩形纸片,若将纸片沿ED折叠,使C落在AD上,点C的对应点为F点,若BC=3EC,DC=5,则( )
如图是一张矩形纸片,若将纸片沿ED折叠,使C落在AD上,点C的对应点为F点,若BC=3EC,DC=5,则( )| A、BE=15 | ||
B、ED=5
| ||
| C、EC≠DC | ||
| D、ED=10 |
考点:翻折变换(折叠问题)
专题:计算题
分析:根据折叠的性质得DF=DC=5,∠C=∠DFE=90°,可判断四边形DCEF为正方形,根据正方形的性质得CE=CD=5,而BC=3EC,所以BE=10,DE=
CD=5
.
| 2 |
| 2 |
解答:解:∵将纸片沿ED折叠,使C落在AD上,点C的对应点为F点,
∴DF=DC=5,∠C=∠DFE=90°,
∴四边形DCEF为正方形,
∴CE=CD=5,
∴BC=3EC=15,DE=
CD=5
,
∴BE=BC-CE=10.
故选B.
∴DF=DC=5,∠C=∠DFE=90°,
∴四边形DCEF为正方形,
∴CE=CD=5,
∴BC=3EC=15,DE=
| 2 |
| 2 |
∴BE=BC-CE=10.
故选B.
点评:本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了正方形的性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
图象经过第二四象限的双曲线所对应的函数可能是下列函数中的( )
| A、y=3x | ||
B、y=
| ||
C、y=-
| ||
| D、y=-3x |
在数轴上表示不等式组
的解,其中正确的是( )
|
A、 |
B、 |
C、 |
D、 |
 如图,已知线段AB=4,延长线段AB至C,使BC=2AB,点D是AC的中点,则DC=( )
如图,已知线段AB=4,延长线段AB至C,使BC=2AB,点D是AC的中点,则DC=( )| A、5 | B、6 | C、7 | D、8 |
 如图下列条件不能得到AD∥BC的是( )
如图下列条件不能得到AD∥BC的是( )| A、∠D+∠BCD=180° |
| B、∠1=∠4 |
| C、∠2=∠3 |
| D、∠D=∠5 |
已知关于x,y的方程组
的解满足x+y=3,则k的值为( )
|
A、
| ||
B、
| ||
C、
| ||
D、
|
不等式组
的所有整数解的和是( )
|
| A、-3 | B、-2 | C、0 | D、-5 |