题目内容
6.解方程组:(1)$\left\{\begin{array}{l}{y=3x-7,①}\\{5x+2y=8,②}\end{array}\right.$ (2)$\left\{\begin{array}{l}{3x-y+z=4,①}\\{2x+3y-z=12,②}\\{x+y+z=6.③}\end{array}\right.$.
分析 (1)方程组利用代入消元法求出解即可;
(2)方程组利用加减消元法求出解即可.
解答 解:(1)把①代入②得:5x+6x-14=8,即x=2,
把x=2代入①得:y=-1,
则方程组的解为$\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$;
(2)①+②得:5x+2y=16④,
②+③得:3x+4y=18⑥,
⑤×2-⑥得:7x=14,即x=2,
把x=2代入④得:y=3,
把x=2,y=3代入③得:z=1,
则方程组的解为$\left\{\begin{array}{l}{x=2}\\{y=3}\\{z=1}\end{array}\right.$.
点评 此题考查了解二元一次方程组,以及解三元一次方程组,熟练掌握运算法则是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.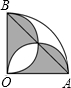 如图,半径为1cm,圆心角为90°的扇形OAB中,分别以OA,OB为直径作半圆,则图中阴影部分的面积为( )
如图,半径为1cm,圆心角为90°的扇形OAB中,分别以OA,OB为直径作半圆,则图中阴影部分的面积为( )
 如图,半径为1cm,圆心角为90°的扇形OAB中,分别以OA,OB为直径作半圆,则图中阴影部分的面积为( )
如图,半径为1cm,圆心角为90°的扇形OAB中,分别以OA,OB为直径作半圆,则图中阴影部分的面积为( )| A. | πcm2 | B. | $\frac{2}{3}$πcm2 | C. | $\frac{1}{2}$cm2 | D. | $\frac{2}{3}$cm2 |
11.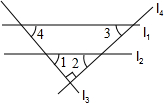 如图,直线l1∥l2,l3⊥l4,有下列三个命题,①∠1+∠3=90°;②∠2+∠3=90°;③∠2=∠4,则( )
如图,直线l1∥l2,l3⊥l4,有下列三个命题,①∠1+∠3=90°;②∠2+∠3=90°;③∠2=∠4,则( )
 如图,直线l1∥l2,l3⊥l4,有下列三个命题,①∠1+∠3=90°;②∠2+∠3=90°;③∠2=∠4,则( )
如图,直线l1∥l2,l3⊥l4,有下列三个命题,①∠1+∠3=90°;②∠2+∠3=90°;③∠2=∠4,则( )| A. | 只有①正确 | B. | 只有②正确 | C. | ①和③正确 | D. | ①②③都正确 |
15. 一只小鸟自由自在地在空中飞行,然后随意落在如图所示的某个方格中(每个方格除颜色外完全一样),那么小鸟停在黑色方格中的概率是( )
一只小鸟自由自在地在空中飞行,然后随意落在如图所示的某个方格中(每个方格除颜色外完全一样),那么小鸟停在黑色方格中的概率是( )
 一只小鸟自由自在地在空中飞行,然后随意落在如图所示的某个方格中(每个方格除颜色外完全一样),那么小鸟停在黑色方格中的概率是( )
一只小鸟自由自在地在空中飞行,然后随意落在如图所示的某个方格中(每个方格除颜色外完全一样),那么小鸟停在黑色方格中的概率是( )| A. | $\frac{1}{2}$ | B. | $\frac{5}{12}$ | C. | $\frac{1}{3}$ | D. | $\frac{7}{12}$ |
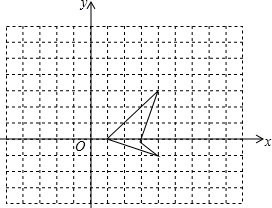 如图,方格纸中有一条美丽可爱的小鱼.
如图,方格纸中有一条美丽可爱的小鱼.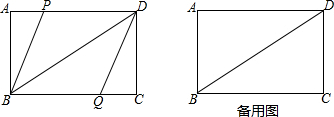
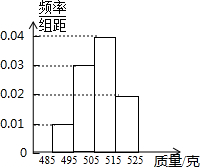 为了检测某自动包装流水线的生产情况,在流水线上随机抽取40件产品,分别称出它们的质量(单位:克)作为样本.如图是样本的频率分布直方图,根据图中各组的组中值估计产品的平均质量507克.
为了检测某自动包装流水线的生产情况,在流水线上随机抽取40件产品,分别称出它们的质量(单位:克)作为样本.如图是样本的频率分布直方图,根据图中各组的组中值估计产品的平均质量507克.