题目内容
18.先化简,再求值:($\frac{{x}^{2}+1}{{x}^{2}-x}$-$\frac{2}{x-1}$)÷$\frac{x+1}{x}$-1,其中x=$\sqrt{2}$.分析 先算括号里面的,再算除法,减法,最后把x的值代入进行计算即可.
解答 解:原式=[$\frac{{x}^{2}+1}{x(x-1)}$-$\frac{2x}{x(x-1)}$]÷$\frac{x+1}{x}$-1
=$\frac{x-1}{x}$•$\frac{x}{x+1}$-1
=$\frac{x-1}{x+1}$-1
=$\frac{x-1-x-1}{x+1}$
=-$\frac{2}{x+1}$,
当x=$\sqrt{2}$时,原式=-$\frac{2}{\sqrt{2}+1}$=-2$\sqrt{2}$+2.
点评 本题考查的是分式的化简求值,分式求值题中比较多的题型主要有三种:转化已知条件后整体代入求值;转化所求问题后将条件整体代入求值;既要转化条件,也要转化问题,然后再代入求值.

练习册系列答案
相关题目
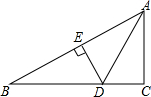 如图,在Rt△ABC中,∠C=90°,∠CAB的平分线交BC于D,DE是AB的垂直平分线,垂足为E,若BC=3,则DE的长为1.
如图,在Rt△ABC中,∠C=90°,∠CAB的平分线交BC于D,DE是AB的垂直平分线,垂足为E,若BC=3,则DE的长为1. 如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-6,0),B(-1,1),C(-3,3),将△ABC绕点B顺时针方向旋转90°后得到△A1BC1.
如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-6,0),B(-1,1),C(-3,3),将△ABC绕点B顺时针方向旋转90°后得到△A1BC1.
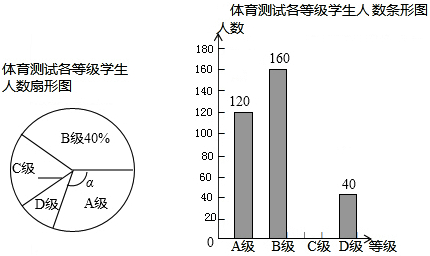
 如图,在四边形ABCD中,∠B=∠D=90°,且AB=CD,四边形ABCD是矩形吗?为什么?
如图,在四边形ABCD中,∠B=∠D=90°,且AB=CD,四边形ABCD是矩形吗?为什么?