题目内容
14. 如图,已知AB⊥BD,CD⊥BD.
如图,已知AB⊥BD,CD⊥BD. (1)若AB=16,CD=9,BD=15,请问在BD上是否存在P点,使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似?若存在,求BP的长;若不存在,请说明理由;
(2)若AB=16,CD=9,BD=24,请问在BD上存在多少个P点,使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似?并求BP的长;
(3)若AB=m,CD=n,BD=l,请问在m、n、l满足什么关系时,存在以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似的三个P点?
分析 (1)设BP=x,则DP=15-x,再分△ABP∽△PDC 与△ABP∽△CDP两种情况进行讨论;
(2)设BP=x,则DP=24-x,再分△ABP∽△PDC 与△ABP∽△CDP两种情况进行讨论;
(3)设BP=x,则DP=l-x,再分△ABP∽△PDC 与△ABP∽△CDP两种情况进行讨论.
解答 解:(1)设BP=x,则DP=15-x
若是△ABP∽△PDC 则$\frac{AB}{PD}$=$\frac{BP}{CD}$,即$\frac{16}{15-x}$=$\frac{x}{9}$,方程无解.
若是△ABP∽△CDP 则$\frac{AB}{CD}$=$\frac{BP}{DP}$,即$\frac{16}{9}$=$\frac{x}{15-x}$,解得x=9.6,
所以BP=9.6;
(2)设BP=x,则DP=24-x
若是△ABP∽△PDC 则$\frac{AB}{PD}$=$\frac{BP}{CD}$,即$\frac{16}{24-x}$=$\frac{x}{9}$,解得x=12,
若是△ABP∽△CDP 则$\frac{AB}{CD}$=$\frac{BP}{DP}$,即$\frac{16}{9}$=$\frac{x}{24-x}$,解得x=15.36.
所以BP=12或15.36;
(3)设BP=x,则DP=l-x,
若是△ABP∽△CDP 则$\frac{AB}{CD}$=$\frac{BP}{DP}$,即$\frac{m}{n}$=$\frac{x}{l-x}$,解之得x=$\frac{ml}{m+n}$,
若是△ABP∽△PDC 则$\frac{AB}{PD}$=$\frac{BP}{CD}$,即$\frac{m}{l-x}$=$\frac{x}{n}$,得方程:x2-lx+mn=0,
当△=l2-4mn>0时,存在以P、A、B为顶点的三角形与以P、C、D为顶点的三角形相似的3个点P.
点评 本题考查的是相似形综合题,涉及到相似三角形的判定与性质,由于此题中相似三角形的对应点不确定故应进行分类讨论.

 若计算器的四个键的序号如图所示,在角的度量单位为“度的状态下”用计算器求sin47°,正确的按键顺序是( )
若计算器的四个键的序号如图所示,在角的度量单位为“度的状态下”用计算器求sin47°,正确的按键顺序是( )| A. | (1)(2)(3)(4) | B. | (2)(4)(1)(3) | C. | (1)(4)(2)(3) | D. | (2)(1)(4)(3) |
 如图,直径为6的半圆绕直径AB的端点A顺时针旋转45°,点B的对应点为B′,则图中阴影部分的面积是( )
如图,直径为6的半圆绕直径AB的端点A顺时针旋转45°,点B的对应点为B′,则图中阴影部分的面积是( )| A. | $\frac{3}{4}π$ | B. | $\frac{9}{4}π$ | C. | $\frac{9}{2}π$ | D. | 9π |
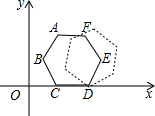 如图的平面直角坐标系中有一个正六边形ABCDEF,其中C、D的坐标分别为(1,0)和(2,0).若在无滑动的情况下,将这个六边形沿着x轴向右滚动,则在滚动过程中,这个六边形的顶点A、B、C、D、E、F中,会过点(50,2)的是点A.
如图的平面直角坐标系中有一个正六边形ABCDEF,其中C、D的坐标分别为(1,0)和(2,0).若在无滑动的情况下,将这个六边形沿着x轴向右滚动,则在滚动过程中,这个六边形的顶点A、B、C、D、E、F中,会过点(50,2)的是点A. 二次函数y=ax2+bx+c的图象如图所示,则下列结论:
二次函数y=ax2+bx+c的图象如图所示,则下列结论: