Question

如图，在平面直角坐标系中，⊙P的圆心坐标是（4，a）（a＞4），半径为4，函数y=x的图象被⊙P截得的弦AB的长为2

15

，则a的值是

 

．

Answer 1

考点：垂径定理,坐标与图形性质,勾股定理,等腰直角三角形

专题：

分析：过P点作PE⊥AB于E，过P点作PC⊥x轴于C，交AB于D，连接PA．分别求出PD、DC，相加即可．

解答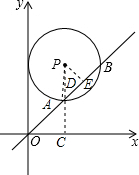：解：过P点作PE⊥AB于E，过P点作PC⊥x轴于C，交AB于D，连接PA．
∵PE⊥AB，AB=2

15

，半径为4，
∴AE=

1

2

AB=

15

，PA=4，
根据勾股定理得：PE=

AP2-AE2

=

42-( 15 )2

=1，
∵点A在直线y=x上，
∴∠AOC=45°，
∵∠DCO=90°，
∴∠ODC=45°，
∴△OCD是等腰直角三角形，
∴OC=CD=4，
∴∠PDE=∠ODC=45°，
∴∠DPE=∠PDE=45°，
∴DE=PE=1，
∴PD=

2

．
∵⊙P的圆心是（4，a），
∴a=PD+DC=

2

+4．
故答案为：4+

2

．

点评：本题考查的是垂径定理，题中运用圆与直线的关系以及直角三角形等知识求出线段的长是解题的关键．注意函数y=x与x轴的夹角是45°．