题目内容
在平面直角坐标系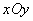 中,⊙C的半径为r,点P是与圆心C不重合的点,给出如下定义:若点
中,⊙C的半径为r,点P是与圆心C不重合的点,给出如下定义:若点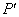 为射线CP上一点,满足
为射线CP上一点,满足
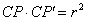 ,则称点
,则称点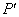 为点P关于⊙C的反演点.右图为点P及其关于⊙C的反演点
为点P关于⊙C的反演点.右图为点P及其关于⊙C的反演点 的示意图.
的示意图.
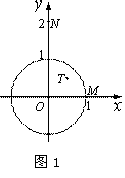
(1) 如图1,当⊙O的半径为1时,分别求出点M(1,0),N(0,2),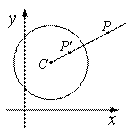
T(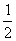 ,
,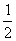 )关于⊙O的反演点
)关于⊙O的反演点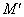 ,
,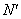 ,
,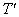 的坐标;
的坐标;
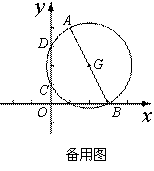
(2) 如图2,已知点A(1,4),B(3,0),以AB为直径的⊙G与y轴交于点C,D(点C位于点D下方),E为CD的中点.
① 若点O,E关于⊙G的反演点分别为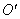 ,
,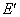 ,求∠
,求∠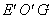 的大小;
的大小;
 ② 若点P在⊙G上,且∠BAP=∠OBC,设直线AP与x轴的交点为Q,点Q关于⊙G的反演点为
② 若点P在⊙G上,且∠BAP=∠OBC,设直线AP与x轴的交点为Q,点Q关于⊙G的反演点为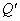 ,请直接写出线段
,请直接写出线段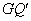 的长度.
的长度.
 | |||
 | |||
 解:(1)
解:(1)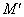 (1,0),
(1,0),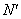 (0,
(0, ),
),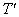 (1,1); ……………………………………3分
(1,1); ……………………………………3分
(2) ①解法一:∵ ,
, ,
,
∴ =
= ,
,
即 .
.
又∵∠ =∠EGO,
=∠EGO,
∴△ ∽△OEG, ……………………………………4分
∽△OEG, ……………………………………4分
∴∠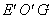 =∠OEG.
=∠OEG.
∵E为弦CD的中点,G为圆心,
∴GE⊥CD于点E,
即∠OEG=90°, ……………………………………5分
∴∠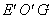 =90°. ……………………………………6分
=90°. ……………………………………6分
解法二:易得G(2,2),E(0,2), ,
,
∴EG=2,OG= .
.
∵ ,
, ,
,
∴ =
= ,
, =
= . ……………………………………4分
. ……………………………………4分
∵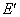 在射线GE上,
在射线GE上,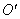 在射线GO上,
在射线GO上,
∴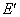 (
( ,2),
,2),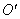 (
( ,
, ),
),
∴ =
= , ……………………………………5分
, ……………………………………5分
∴ ,
,
∴∠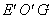 =90°. ……………………………………6分
=90°. ……………………………………6分
②线段 的长度为
的长度为 或
或 .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目


 ;
; ;
; ;
; ;
; ;(用含a、b的代数式表示);
;(用含a、b的代数式表示); ,那么
,那么
 (填 “=”或 “≠”);
(填 “=”或 “≠”); ,请求出
,请求出 的值.
的值.  cos45°-tan30°·sin60°.
cos45°-tan30°·sin60°. ≈1.41,
≈1.41, ≈1.73,
≈1.73, ≈2.45,)
≈2.45,)
 =_______
=_______ .
. ,
, ,
, 平分
平分 .
. 的度数.
的度数.
