题目内容
20.一只不透明的口袋里装有2个红球,4个黄球和m个白球,每个球除颜色外都相同,将球摇匀,从中摸出1个球,若从中摸到白球的概率为$\frac{1}{3}$.(1)求白球的个数;
(2)小明说:“口袋中共有三种颜色的球,所以从袋中任意摸出一球,摸到红球、白球或黄球的概率都是$\frac{1}{3}$”.请你判断小明的说法正确吗?为什么?
分析 (1)根据“口袋里装有2个红球,4个黄球和m个白球,每个球除颜色外都相同,将球摇匀,从中摸出1个球,若从中摸到白球的概率为$\frac{1}{3}$”得:$\frac{m}{m+4+2}$=$\frac{1}{3}$,则可求得答案;
(2)分别求得摸到红球、白球或黄球的概率,即可知小明的说法错误.
解答 解:(1)设口袋中白球的个数为m,
根据题意得:$\frac{m}{m+4+2}$=$\frac{1}{3}$,
解得:m=3;
答:白球的个数为3个;
(2)不正确.
∵P(白球)=$\frac{1}{3}$,P(红球)=$\frac{2}{9}$,P(黄球)=$\frac{4}{9}$;
∴小明的说法不正确.
点评 此题考查了概率的求法:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=$\frac{m}{n}$.

练习册系列答案
相关题目



 如图,在第1个△ABA1中,∠B=20°,∠BAA1=∠BA1A,在A1B上取一点C,延长AA1到A2,使得在第2个△A1CA2中,∠A1CA2=∠A1A2C;在A2C上取一点D,延长A1A2到A3,使得在第3个△A2DA3中,∠A2DA3=∠A2A3D;…,按此做法进行下去,第三个三角形中,以A3为顶点的底角的度数为20°;第n个三角形中以An为顶点的底角的度数为$\frac{80°}{{2}^{n-1}}$.
如图,在第1个△ABA1中,∠B=20°,∠BAA1=∠BA1A,在A1B上取一点C,延长AA1到A2,使得在第2个△A1CA2中,∠A1CA2=∠A1A2C;在A2C上取一点D,延长A1A2到A3,使得在第3个△A2DA3中,∠A2DA3=∠A2A3D;…,按此做法进行下去,第三个三角形中,以A3为顶点的底角的度数为20°;第n个三角形中以An为顶点的底角的度数为$\frac{80°}{{2}^{n-1}}$.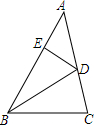 如图,BD是△ABC的角平分线,DE⊥AB,垂足为E,AB=16,BC=12.
如图,BD是△ABC的角平分线,DE⊥AB,垂足为E,AB=16,BC=12.