题目内容
1.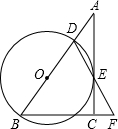 如图,在 Rt△ABC中,∠ACB=90°,D是AB边上的一点,以BD为直径的⊙O与边AC相切于点E,连结DE并延长,与BC的延长线交于点 F.
如图,在 Rt△ABC中,∠ACB=90°,D是AB边上的一点,以BD为直径的⊙O与边AC相切于点E,连结DE并延长,与BC的延长线交于点 F.(1)求证:BD=BF;
(2)若 EF=6,CF=3,求⊙O的半径长.
分析 (1)连接OE,由切线的性质可证明OE∥BC,再结合OD=OE,可证明∠BDF=∠F,可证得BD=BF;
(2)在Rt△CEF中可证得∠F=60°,结合(1)的结论可证明△BDF为等边三角形,连接BE,则E为DF的中点,可求得DF,则可求得BD,可求得⊙O的半径.
解答 (1)证明:
如图1,连接OE,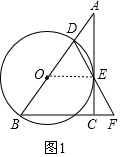
∵AC是⊙O的切线,
∴OE⊥AC,
∵∠ACB=90°,
∴OE∥BF,
∴∠OED=∠F,
∵OE=OD,
∴∠ODE=∠OED,
∴∠ODF=∠F,
∴BD=BF;
(2)解:
如图2,连接BE,
∵BD为⊙O的直径,
∴BE⊥DF,
∴DE=EF=6,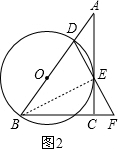
∵CF=3,EF=6,
∴cos∠F=$\frac{CF}{EF}$=$\frac{3}{6}$=$\frac{1}{2}$,
∴∠F=60°,
又由(1)可知BD=BF,
∴△BDF为等边三角形,
∴BD=DF=12,
∴⊙O的半径为6.
点评 本题主要考查切线的性质及等边三角形的判定和性质,在(1)中证得∠ODE=∠F是解题的关键,在(2)中求得△BDF为等边三角形是解题的关键.

练习册系列答案
相关题目
12.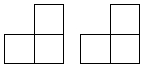 由一些大小相同的小正方形组成,下面的两个图分别是从正面和从上面看这个几何体得到的平面图形,那么组成该几何体所需的小正方形的个数为( )
由一些大小相同的小正方形组成,下面的两个图分别是从正面和从上面看这个几何体得到的平面图形,那么组成该几何体所需的小正方形的个数为( )
 由一些大小相同的小正方形组成,下面的两个图分别是从正面和从上面看这个几何体得到的平面图形,那么组成该几何体所需的小正方形的个数为( )
由一些大小相同的小正方形组成,下面的两个图分别是从正面和从上面看这个几何体得到的平面图形,那么组成该几何体所需的小正方形的个数为( )| A. | 4个 | B. | 4个或5个 | C. | 5个或6个 | D. | 6个 |
9.矩形的对角线长10cm,顺次连结矩形四边中点所得四边形的周长为( )
| A. | 40 cm | B. | 10 cm | C. | 5 cm | D. | 20 cm |
16. 在扇形OACB中,∠AOB=120°,⊙O′为弓形ACB的最大的内切圆,若AB的长为2π,则⊙O′的周长为( )
在扇形OACB中,∠AOB=120°,⊙O′为弓形ACB的最大的内切圆,若AB的长为2π,则⊙O′的周长为( )
 在扇形OACB中,∠AOB=120°,⊙O′为弓形ACB的最大的内切圆,若AB的长为2π,则⊙O′的周长为( )
在扇形OACB中,∠AOB=120°,⊙O′为弓形ACB的最大的内切圆,若AB的长为2π,则⊙O′的周长为( )| A. | π | B. | $\frac{2}{3}$π | C. | $\frac{3}{2}$π | D. | 2π |
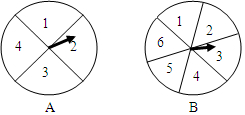 如图,有两个可以自由转动的转盘A、B,转盘A被均匀分成4等份,每份标上数字1、2、3、4四个数字;转盘B被均匀地分成6等份,每份分别标上1,2,3,4,5,6六个数字.有人为甲乙两人设计了一个游戏,其规则如下:
如图,有两个可以自由转动的转盘A、B,转盘A被均匀分成4等份,每份标上数字1、2、3、4四个数字;转盘B被均匀地分成6等份,每份分别标上1,2,3,4,5,6六个数字.有人为甲乙两人设计了一个游戏,其规则如下: 如图,已知线段MN为正六边形ABCDEF平移后得到的一条边,请画出平移后的图形.
如图,已知线段MN为正六边形ABCDEF平移后得到的一条边,请画出平移后的图形.