题目内容
已知抛物线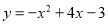
．（1）求出这个抛物线的对称轴和顶点坐标；（2）在给定的坐标系中画出这个抛物线，若抛物线与x轴交于A，B两点，与y轴交于点C，求△ABC的面积．
（1）顶点：（2,1） 对称轴：直线x=2 （2）3.
【解析】
试题分析：首先将抛物线的解析式化简成顶点式，然后根据顶点式求出顶点坐标和对称轴；分别求出函数与x轴和y轴的交点坐标，然后计算面积.
试题解析：（1）
=－
+1
∴顶点坐标是（2,1），对称轴是直线x=2．
（2）图象如图所示：
令y=0，
， 
， 
，
∴A（1,0），B（3,0）．
又∵C（0,-3）， ∴AB=2，OC=3，
∴
．
考点：二次函数的顶点坐标、与坐标轴的交点坐标、三角形的面积求法.
练习册系列答案
手拉手全优练考卷系列答案
相关题目
、
是方程
的两根，则代数式
= .
B．
C．
D．
，则
的值为（ ） 
B．
C．
D．
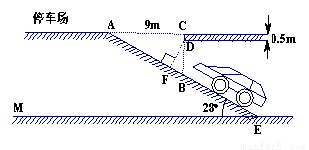
的图象如图，点A0位于坐标原点，点A1，A2，A3…An在y轴的正半轴上，点B1，B2，B3…Bn在二次函数位于第一象限的图象上，点C1，C2，C3…Cn在二次函数位于第二象限的图象上，四边形A0B1A1C1，四边形A1B2A2C2，四边形A2B3A3C3…四边形An﹣1BnAnCn都是菱形，∠A0B1A1=∠A1B2A2=∠A2B3A3…=∠An﹣1BnAn=60°，菱形An﹣1BnAnCn的周长为 ．
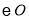于点B，联结PO并延长交
的切线；
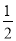，求