Question

9．如图，已知⊙O₁、⊙O₂相交于A、B两点，直线O₁O₂交两圆于C、D两点．若∠O₁AO₂=40°，则∠CBD等于（　　）

• A． 110°
• B． 120°
• C． 130°
• D． 140°

Answer 1

分析 先证明△AO₁O₂≌△BO₁O₂，求出∠O₁BC+∠O₂BD=70°，根据∠CBD=∠CBO₁+∠O₁BO₂+∠O₂BD即可解决问题．

解答 解：如图，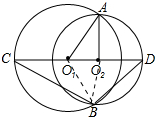
在△AO₁O₂和△BO₁O₂中，
$\left\{\begin{array}{l}{A{O}_{1}=B{O}_{1}}\\{A{O}_{2}=B{O}_{2}}\\{{O}_{1}{O}_{2}={O}_{1}{O}_{2}}\end{array}\right.$，
∴△AO₁O₂≌△BO₁O₂，
∴∠AO₂O₁=∠BO₂O₁，∠AO₁O₂=∠BO₁O₂，∠O₁AO₁=∠O₁BO₂=40°，
∴∠AO₁O₂+∠AO₂O₁=∠BO₁O₂+∠BO₂O₁=140°，
∵O₁C=O₁B，O₂B=O₂D，
∴∠O₁CB=∠O₁BC，∠O₂BD=∠O₂DB，
∴2∠O₁BC+2∠O₂BD=140°，
∴∠O₁BC+∠O₂BD=70°，
∴∠CBD=∠CBO₁+∠O₁BO₂+∠O₂BD=110°．
故选A．

点评 本题考查相交两个圆的性质、全等三角形的判定和性质、等腰三角形的判定和性质等知识，解题的关键是利用三角形的外角的性质求得∠O₁BC+∠O₂BD=70°，属于中考常考题型．