题目内容
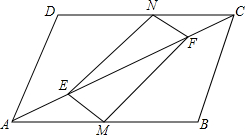 如图,在平行四边形ABCD中,M,N分别是AB,CD的中点,E,F是AC上两点,且AE=CF.
如图,在平行四边形ABCD中,M,N分别是AB,CD的中点,E,F是AC上两点,且AE=CF.求证:四边形MFNE是平行四边形.
考点:平行四边形的判定与性质
专题:证明题
分析:连接MN交AC于点O,可证得MN∥AD,可得O为AC和MN的中点,且可证明OE=OF,可证得结论.
解答:证明:连接MN交AC于点O,
∵M、N分别是AB、CD的中点,
∴DN=
CD,AM=
AB,
又∵四边形ABCD为平行四边形,
∴AB=CD,且AB∥CD,
∴DN=AM,且DN∥AM,
∴四边形AMND为平行四边形,
∴MN∥AD,
∴O为AC的中点,
∴ON=OM=
AD,OA=OC,
∵AE=CF,
∴OE=OF,
∴四边形MFNE为平行四边形.
∵M、N分别是AB、CD的中点,
∴DN=
| 1 |
| 2 |
| 1 |
| 2 |
又∵四边形ABCD为平行四边形,
∴AB=CD,且AB∥CD,
∴DN=AM,且DN∥AM,
∴四边形AMND为平行四边形,
∴MN∥AD,
∴O为AC的中点,
∴ON=OM=
| 1 |
| 2 |
∵AE=CF,
∴OE=OF,
∴四边形MFNE为平行四边形.
点评:本题主要考查平行四边形的判定和性质,掌握平行四边形的判定方法是解题的关键.即①有两组对边分别平行的四边形是平行四边形,②有两组对边分别相等的四边形是平行四边形,③有一组对边平行且相等的四边形是平行四边形,④有两组对角分别相等的四边形是平行四边形,⑤对角线互相平分的四边形是平行四边形.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
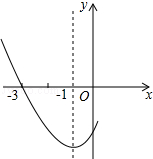 如图是二次函数y=ax2+bx+c图象的一部分,其对称轴是x=-1,且过点(-3,0),下列说法:①abc<0;②2a-b=0;③4a+2b+c<0;④若(-5,y1),(3,y2)是抛物线上两点,则y1<y2,其中说法正确的是( )
如图是二次函数y=ax2+bx+c图象的一部分,其对称轴是x=-1,且过点(-3,0),下列说法:①abc<0;②2a-b=0;③4a+2b+c<0;④若(-5,y1),(3,y2)是抛物线上两点,则y1<y2,其中说法正确的是( )| A、①② | B、②③ |
| C、①②④ | D、②③④ |
已知x=2是2x+a=5的解,则a的值为( )
| A、1 | ||
B、
| ||
| C、-1 | ||
D、
|
 如图,在矩形ABCD中,E,F是BC上的两点,且BE=CF,连接AF,FD,相交于点P.求证:PA=PD.
如图,在矩形ABCD中,E,F是BC上的两点,且BE=CF,连接AF,FD,相交于点P.求证:PA=PD. 如图,直角三角形DEF是由直角三角形ABC沿BC向右平移3cm得到的,如果AB=6cm,DH=2cm,求图中阴影部分的面积.
如图,直角三角形DEF是由直角三角形ABC沿BC向右平移3cm得到的,如果AB=6cm,DH=2cm,求图中阴影部分的面积.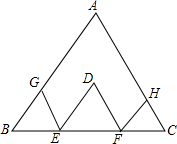 如图,D为△ABC内一点,过D作DE∥AB,DF∥AC,分别交BC于点E,F,过E作EG∥AC,交AB于点G,过F作FH∥AB,交AC于H.求证:BG+GE+ED+DF+FH+HC=AB+AC.
如图,D为△ABC内一点,过D作DE∥AB,DF∥AC,分别交BC于点E,F,过E作EG∥AC,交AB于点G,过F作FH∥AB,交AC于H.求证:BG+GE+ED+DF+FH+HC=AB+AC. 已知:如图,∠AHF+∠FMD=180°,GH平分∠AHM,MN平分∠DMH.求证:GH∥MN.
已知:如图,∠AHF+∠FMD=180°,GH平分∠AHM,MN平分∠DMH.求证:GH∥MN.