题目内容
 如图,在矩形ABCD中,E,F是BC上的两点,且BE=CF,连接AF,FD,相交于点P.求证:PA=PD.
如图,在矩形ABCD中,E,F是BC上的两点,且BE=CF,连接AF,FD,相交于点P.求证:PA=PD.考点:矩形的性质,全等三角形的判定与性质
专题:证明题
分析:首先证明△ABF≌△DCE可得∠BAF=∠CDE,然后再根据矩形的性质可得∠BAD=∠CDA=90°,进而可证出∠DAF=∠ADE,根据等角对等边可得AP=DP.
解答:证明:∵BE=CF,
∴BE+EF=FC+EF,
即BF=EC,
∵四边形ABCD是矩形,
∴∠B=∠C=90°,AB=CD,∠BAD=∠CDA=90°,
在△ABF和△DCE中,
,
∴△ABF≌△DCE(SAS),
∴∠BAF=∠CDE,
∴∠DAF=∠ADE,
∴AP=DP.
∴BE+EF=FC+EF,
即BF=EC,

∵四边形ABCD是矩形,
∴∠B=∠C=90°,AB=CD,∠BAD=∠CDA=90°,
在△ABF和△DCE中,
|
∴△ABF≌△DCE(SAS),
∴∠BAF=∠CDE,
∴∠DAF=∠ADE,
∴AP=DP.
点评:此题主要考查了矩形的性质,关键是掌握矩形四个角都是直角.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
两条直线被第三条直线所截,若有一对内错角相等,则这对内错角的角平分线( )
| A、互相垂直 |
| B、相交但不垂直 |
| C、互相平行 |
| D、位置关系无法确定 |
下列描述不正确的是( )
A、单项式-
| ||||
| B、用一个平面去截一个圆柱,截面的形状可能是一个长方形 | ||||
| C、过七边形的一个顶点有5条对角线 | ||||
| D、五棱柱有7个面,15条棱 |
 如图所示,要使一个六边形木架在同一平面内不变形,至少还要再钉上几根木条?要使一个n边形(n≥4)木架在同一平面内不变形,至少还要再钉上几根木条?
如图所示,要使一个六边形木架在同一平面内不变形,至少还要再钉上几根木条?要使一个n边形(n≥4)木架在同一平面内不变形,至少还要再钉上几根木条? 如图,在四边形ABCD中,∠A+∠C=180°,∠B=100°,∠ADE是四边形ABCD的一个外角,则∠ADE=
如图,在四边形ABCD中,∠A+∠C=180°,∠B=100°,∠ADE是四边形ABCD的一个外角,则∠ADE= 如图,在△ABC中,AB=AC,若点P为BC延长线上一点,猜一猜:P到两腰的距离之差等于什么?请给出证明.
如图,在△ABC中,AB=AC,若点P为BC延长线上一点,猜一猜:P到两腰的距离之差等于什么?请给出证明. 甲、乙两名自行车爱好者准备在一段长为3400m的笔直公路上进行比赛,比赛开始时乙在起点,甲在乙的前面,他们同时出发,匀速前进,已知甲的速度为15m/s,设甲、乙两人之间的距离为y(米),比赛时间为x(秒),图中的折线表示从两人出发至乙先到达终点的过程中y (米)与x(秒)的函数关系,根据图中信息,乙到终点时,甲离终点还有
甲、乙两名自行车爱好者准备在一段长为3400m的笔直公路上进行比赛,比赛开始时乙在起点,甲在乙的前面,他们同时出发,匀速前进,已知甲的速度为15m/s,设甲、乙两人之间的距离为y(米),比赛时间为x(秒),图中的折线表示从两人出发至乙先到达终点的过程中y (米)与x(秒)的函数关系,根据图中信息,乙到终点时,甲离终点还有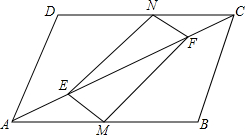 如图,在平行四边形ABCD中,M,N分别是AB,CD的中点,E,F是AC上两点,且AE=CF.
如图,在平行四边形ABCD中,M,N分别是AB,CD的中点,E,F是AC上两点,且AE=CF.