题目内容
11.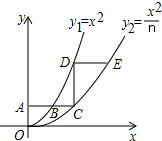 如图,平行于x轴的直线AC分别交函数y1=x2(x≥0)与y2=$\frac{{x}^{2}}{n}$(x≥0)的图象于B、C两点,过点C作y轴的平行线交y1的图象于点D,直线DE∥AC,交y2的图象于点E,当n=2时,$\frac{DE}{AB}$的值为2-$\sqrt{2}$;当n=k时,$\frac{DE}{AB}$的值为k-$\sqrt{k}$.
如图,平行于x轴的直线AC分别交函数y1=x2(x≥0)与y2=$\frac{{x}^{2}}{n}$(x≥0)的图象于B、C两点,过点C作y轴的平行线交y1的图象于点D,直线DE∥AC,交y2的图象于点E,当n=2时,$\frac{DE}{AB}$的值为2-$\sqrt{2}$;当n=k时,$\frac{DE}{AB}$的值为k-$\sqrt{k}$.
分析 设C(t,$\frac{{t}^{2}}{n}$),利用AC∥x轴得到B点的纵坐标为$\frac{{t}^{2}}{n}$,再根据抛物线上点的坐标特征得到B($\frac{\sqrt{n}}{n}$t,$\frac{{t}^{2}}{n}$);同样可确定D(t,t2),E($\sqrt{n}$t,t2),则AB=$\frac{\sqrt{n}}{n}$,DE=($\sqrt{n}$-1)t,于是可计算出$\frac{DE}{AB}$=n-$\sqrt{n}$,然后把n=2和k代入计算即可.
解答 解:设C(t,$\frac{{t}^{2}}{n}$),
∵AC∥x轴,
∴B点的纵坐标为$\frac{{t}^{2}}{n}$,
当y=$\frac{{t}^{2}}{n}$时,$\frac{{t}^{2}}{n}$=x2,解得x=$\frac{t}{\sqrt{n}}$=$\frac{\sqrt{n}}{n}$t,
∴B($\frac{\sqrt{n}}{n}$t,$\frac{{t}^{2}}{n}$);
∴AB=$\frac{\sqrt{n}}{n}$t,
∵CD∥y轴,
∴点D的横坐标为t,
∴D(t,t2),
∵DE∥x轴,
∴E点的纵坐标为t2,
当y=t2时,$\frac{{x}^{2}}{n}$=t2,解得x=$\sqrt{n}$t,
∴E($\sqrt{n}$t,t2),
∴DE=($\sqrt{n}$-1)t,
∴$\frac{DE}{AB}$=$\frac{(\sqrt{n}-1)t}{\frac{\sqrt{n}t}{n}}$=n-$\sqrt{n}$,
当n=2时,$\frac{DE}{AB}$=2-$\sqrt{2}$;
当n=k时,$\frac{DE}{AB}$=k-$\sqrt{k}$.
故答案为2-$\sqrt{2}$;k-$\sqrt{k}$.
点评 本题考查了二次函数图象上点的坐标特征:二次函数图象上点的坐标满足其解析式.

①若a≠b,则a2≠b2;
②对于不为零的实数c,关于x的方程x+$\frac{c}{x}$=c+1的根是c;
③过一点有且只有一条直线与已知直线平行;
④在反比例函数y=$\frac{2}{x}$中,如果自变量x>2,那么函数值y<1.
是假命题的个数是( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
| A. | 可以是x=-0.2,不可以是 x=0.2 | |
| B. | 可以是x=0.2,不可以是 x=-0.2 | |
| C. | 可以是x=-0.2,也可以是 x=0.2 | |
| D. | 既不可以是x=-0.2,也不可以是 x=0.2 |
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{2}{3}$ |
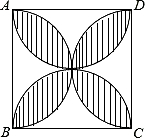 如图,正方形的边长为2,以各边为直径在正方形内画半圆,则图中阴影部分的面积( )
如图,正方形的边长为2,以各边为直径在正方形内画半圆,则图中阴影部分的面积( )| A. | π-4 | B. | 2π-4 | C. | 4-π | D. | 4-2π |
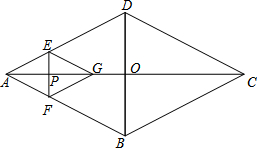 菱形ABCD的对角线AC,BD相交于点O,AC=16,BD=12,动点P在线段AC上从点A向点C以4个单位/秒的速度运动,过点P作EF⊥AC,交菱形ABCD的边于点E、F,在直线AC上有一点G,使△AEF与△GEF关于EF对称.设菱形ABCD被四边形AEGF盖住部分的面积为S1,未被盖住部分的面积为S2,点P运动时间为x秒.
菱形ABCD的对角线AC,BD相交于点O,AC=16,BD=12,动点P在线段AC上从点A向点C以4个单位/秒的速度运动,过点P作EF⊥AC,交菱形ABCD的边于点E、F,在直线AC上有一点G,使△AEF与△GEF关于EF对称.设菱形ABCD被四边形AEGF盖住部分的面积为S1,未被盖住部分的面积为S2,点P运动时间为x秒.