题目内容
20.若二次函数y=ax2-4x+a的图象与x轴有交点,其中a为非负整数,则a=1或2.分析 首先判断二次函数二次项系数不为0,然后根据二次函数y=ax2-4x+a的图象与x轴有交点,根据△≥0列出a的不等式,求出a的取值范围即可.
解答 解:∵二次函数y=ax2-4x+a是二次函数,
∴a≠0,
∵二次函数y=ax2-4x+a的图象与x轴有交点,
∴△=16-4a2≥0,
∴-2≤a≤2,
∵a为非负整数,
∴a=1或2,
故答案为1或2.
点评 本题主要考查了抛物线与x轴交点的知识,解答本题的关键是根据二次函数y=ax2-4x+a的图象与x轴有交点列出a的不等式,此题难度不大.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案
相关题目
10.若一个棱长均为a的三棱柱,它的主视图和俯视图分别是正方形和正三角形,则它的左视图的面积为( )
| A. | $\frac{\sqrt{3}}{2}$a2 | B. | $\frac{\sqrt{3}}{4}$a2 | C. | $\sqrt{3}$a2 | D. | a2 |
15.在y=□x2□4x□4的□中,任意填上“+”或“-”,可组成若干个不同的二次函数,其中其图象与x轴只有一个交点的概率是( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | 1 |
12.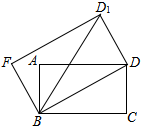 如图,BC=$\sqrt{3}$,以BC为边作矩形ABCD,使∠DBC=30°,得BD=2,再以BD为边作矩形BDD1F,使∠DBD1=30°,得BD1=$\frac{4}{3}\sqrt{3}$,…,依此法继续作下去,则BD4的长为( )
如图,BC=$\sqrt{3}$,以BC为边作矩形ABCD,使∠DBC=30°,得BD=2,再以BD为边作矩形BDD1F,使∠DBD1=30°,得BD1=$\frac{4}{3}\sqrt{3}$,…,依此法继续作下去,则BD4的长为( )
 如图,BC=$\sqrt{3}$,以BC为边作矩形ABCD,使∠DBC=30°,得BD=2,再以BD为边作矩形BDD1F,使∠DBD1=30°,得BD1=$\frac{4}{3}\sqrt{3}$,…,依此法继续作下去,则BD4的长为( )
如图,BC=$\sqrt{3}$,以BC为边作矩形ABCD,使∠DBC=30°,得BD=2,再以BD为边作矩形BDD1F,使∠DBD1=30°,得BD1=$\frac{4}{3}\sqrt{3}$,…,依此法继续作下去,则BD4的长为( )| A. | $\frac{16}{3}\sqrt{3}$ | B. | $\frac{32}{9}$ | C. | $\frac{{32\sqrt{3}}}{9}$ | D. | $\frac{16}{3}$ |
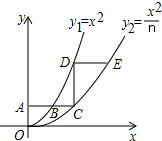 如图,平行于x轴的直线AC分别交函数y1=x2(x≥0)与y2=$\frac{{x}^{2}}{n}$(x≥0)的图象于B、C两点,过点C作y轴的平行线交y1的图象于点D,直线DE∥AC,交y2的图象于点E,当n=2时,$\frac{DE}{AB}$的值为2-$\sqrt{2}$;当n=k时,$\frac{DE}{AB}$的值为k-$\sqrt{k}$.
如图,平行于x轴的直线AC分别交函数y1=x2(x≥0)与y2=$\frac{{x}^{2}}{n}$(x≥0)的图象于B、C两点,过点C作y轴的平行线交y1的图象于点D,直线DE∥AC,交y2的图象于点E,当n=2时,$\frac{DE}{AB}$的值为2-$\sqrt{2}$;当n=k时,$\frac{DE}{AB}$的值为k-$\sqrt{k}$.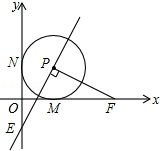 已知在平面直角坐标系xOy中,O是坐标原点,以 P(1,1)为圆心的⊙P与x轴,y轴分别相切于点M和点N,点F从点M出发,沿x轴正方向以每秒1个单位长度的速度运动,连接PF,过点PE⊥PF交y轴于点E,设点F运动的时间是t秒(t>0),作点F关于点M的对称点F′,经过M、E和F′三点的抛物线的对称轴交x轴于点Q,连接QE.在点F运动过程中,是否存在某一时刻,使得以点Q、O、E为顶点的三角形与以点P、M、F为顶点的三角形相似,则t的值为$\sqrt{2}$,$\frac{1+\sqrt{17}}{4}$,2±$\sqrt{2}$,.
已知在平面直角坐标系xOy中,O是坐标原点,以 P(1,1)为圆心的⊙P与x轴,y轴分别相切于点M和点N,点F从点M出发,沿x轴正方向以每秒1个单位长度的速度运动,连接PF,过点PE⊥PF交y轴于点E,设点F运动的时间是t秒(t>0),作点F关于点M的对称点F′,经过M、E和F′三点的抛物线的对称轴交x轴于点Q,连接QE.在点F运动过程中,是否存在某一时刻,使得以点Q、O、E为顶点的三角形与以点P、M、F为顶点的三角形相似,则t的值为$\sqrt{2}$,$\frac{1+\sqrt{17}}{4}$,2±$\sqrt{2}$,. 已知,如图,在平面直角坐标系内,点A的坐标为(0,24),经过原点的直线l1与经过点A的直线l2相交于点B,点B坐标为(18,6).
已知,如图,在平面直角坐标系内,点A的坐标为(0,24),经过原点的直线l1与经过点A的直线l2相交于点B,点B坐标为(18,6). 已知:如图,锐角△ABC的两条高BD、CE相交于点O,且BD=CE.求证:△ABC是等腰三角形.
已知:如图,锐角△ABC的两条高BD、CE相交于点O,且BD=CE.求证:△ABC是等腰三角形.