题目内容
14. 如图,已知抛物线的顶点坐标为M(1,4),且经过点N(2,3),与x轴交于A、B两点(点A在点B左侧),与y轴交于点C.
如图,已知抛物线的顶点坐标为M(1,4),且经过点N(2,3),与x轴交于A、B两点(点A在点B左侧),与y轴交于点C.(1)求抛物线的解析式;
(2)若直线y=kx+t经过C、M两点,且与x轴交于点D,试证明四边形CDAN是平行四边形;
(3)点P在抛物线的对称轴x=1上运动,请探索:在x轴上方是否存在这样的P点,使以P为圆心的圆经过A、B两点,并且与直线CD相切?若存在,请求出点P的坐标;若不存在,请说明理由.
分析 (1)根据待定系数法,可得函数解析式;
(2)根据待定系数法,可得CD的解析式,根据自变量与函数值的对应关系,可得A、D点的坐标,根据一组对边平行且相等的四边形是平行四边形,可得答案;
(3)根据根据勾股定理,可得PA的长,PQ的长,根据圆的半径相等,可得关于u的方程,根据解方程,可得答案.
解答 (1)解:由抛物线的顶点是M(1,4),
设解析式为y=a(x-1)2+4(a<0),
又∵抛物线经过点N(2,3),
∴3=a(2-1)2+4,解得a=-1.
故所求抛物线的解析式为y=-(x-1)2+4=-x2+2x+3;
(2)证明:如图1: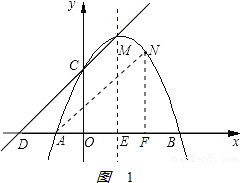 ,
,
直线y=kx+t经过C(0,3)、M(1,4)两点,
$\left\{\begin{array}{l}{t=3}\\{k+t=4}\end{array}\right.$,
即k=1,t=3,
直线CD的解析式为y=x+3,
当y=0时,x=-3,即D(-3,0);
当y=0时,-x2+2x+3=0,解得x=-1,即A(-1,0),
∴AD=2.
∵C(0,3),N(2,3)
∴CN=2=AD,且CN∥AD
∴四边形CDAN是平行四边形.
(3)解:如图2: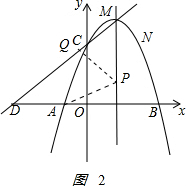 ,
,
假设在x轴上方存在这样的P点,使以P为圆心的圆经过A、B两点,并且与直线CD相切,设P(1,u)其中u>0,
则PA是圆的半径且PA2=u2+22,
过P做直线CD的垂线,垂足为Q,则PQ=PA时以P为圆心的圆与直线CD相切.
由第(2)小题易得:△MDE为等腰直角三角形,故△PQM也是等腰直角三角形,
由P(1,u)得PE=u,PM=|4-u|,PQ=$\frac{\sqrt{2}}{2}$PM.
由PQ2=PA2得方程:
$\frac{1}{2}$(4-u)2=u2+22,
解得u=$\frac{-8+4\sqrt{7}}{2}$,u=$\frac{-8-4\sqrt{7}}{2}$(不符合题意,舍).
所以,满足题意的点P存在,其坐标为(1,$\frac{-8+4\sqrt{7}}{2}$).
点评 本题考查了二次函数综合题,利用待定系数法求函数解析式;利用一组对边平行且相等的四边形是平行四边形;利用等腰直角三角形得出PQ的长是解题关键,又利用半径相等得出关于u的方程.

 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案| A. | 第8秒 | B. | 第10秒 | C. | 第12秒 | D. | 第14秒 |
| A. | 2.03kg | B. | 2.02kg | C. | 2.0kg | D. | 2kg |
 如图,有一路灯杆AB高8m,在路灯下,身高1.6m的小明在距B点6m的点D处测得自己的影长DH,沿BD方向再走14m到达点F处,再测得自己的影长FG.小明身影的长度是变短了还是变长了?变短或变长了多少米?
如图,有一路灯杆AB高8m,在路灯下,身高1.6m的小明在距B点6m的点D处测得自己的影长DH,沿BD方向再走14m到达点F处,再测得自己的影长FG.小明身影的长度是变短了还是变长了?变短或变长了多少米? 如图,在△ADC中,AD=BD=BC,∠C=30°,则∠ADB=60°.
如图,在△ADC中,AD=BD=BC,∠C=30°,则∠ADB=60°.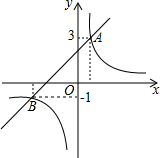 如图,直线y1=x+2与双曲线${y_2}=\frac{k}{x}$相交于A,B两点其中点A的纵坐标为3,点B的纵坐标为-1.
如图,直线y1=x+2与双曲线${y_2}=\frac{k}{x}$相交于A,B两点其中点A的纵坐标为3,点B的纵坐标为-1.